Codechef April Challenge 2019 游记

Subtree Removal

题目大意：

一棵$n(n\le10^5)$个结点的有根树，每个结点有一个权值$w_i(|w_i\le10^9|)$。你可以进行若干次（包括$0$次）操作，每次你可以选择一个连通块，将其删去。若你的操作次数为$k$，则总收益为剩下结点权值之和$-X\cdot k$。求最大总收益。

思路：

树形DP，$f_x$表示以$x$为根的子树的最大总收益。转移时$f_x=w_x+\sum_{y\in{\rm children}_x}f_y$。若$f_x<-X$，则令$f_x=-X$。

时间复杂度$\mathcal O(n)$。

源代码见提交记录。

Playing with Numbers

题目大意：

一棵$n(n\le10^5)$个结点的有根树，每个结点有一个权值$v_i$和一个额外的属性$m_i$。对于一个叶子结点$l_i$，定义其答案为：

对于从根节点到$l_i$的路径上的每个节点，选择一个非负整数，乘以节点的点权。
对路径上所有节点按照上述方式算出来的值求和。
叶子$l_i$的答案就是和对$m_{l_i}$取模的最大值。

求每个叶子节点的答案。

思路：

一个结论是，若干个数$\{A_1,A_2,\ldots,A_k\}$在模$m$意义下，能组合出的最大数为$m-\gcd(A_1,A_2,\ldots,A_k,m)$。

只需一次DFS求出$l_i$到根结点链上的$\gcd$，然后套用上述结论即可。

时间复杂度$\mathcal O(n\log v_i)$。

源代码见提交记录。

Kira Loves Palindromes

题目大意：

给定字符串$S(|S|\le1000,S_i\in[\texttt{'a'},\texttt{'z'}])$，请求出有多少种方案可以从该字符串中选出两个不相交的非空子串（记为$s_1$和$s_2$），使得其串接$s_1+s_2$为回文串。

我们认为$(s_1,s_2)$和$(s^′_1,s^′_2)$是不同的两种方案，当且仅当$s_1$和$s^′_1$的位置不同，或者$s_2$和$s^′_2$的位置不同。

思路：

如图所示：

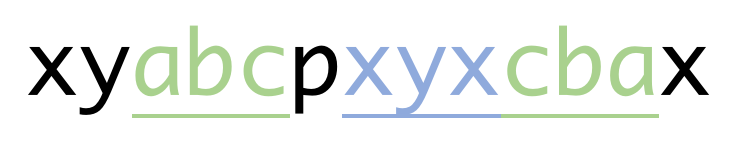
$s_1=\texttt{'abc'},s_2=\texttt{'xyxcba'}$，其中$\texttt{'abc'}$和$\texttt{'cba'}$是对应的部分，而$\texttt{'xyx'}$是插入在中间的回文串。

枚举两个$\texttt{'c'}$的位置$p$和$q$，二分出从$p$和$q$往两侧扩展出的最长距离$len$，对于插入串$S_{[l,r]}$，预处理出满足$l=p+1$且$r<q-1$或$r=q-1$且$l>p+1$的回文串个数$cnt$（注意这里不考虑$l=p+1$且$r=q-1$的情况，避免算重）。对于固定的$p,q$，答案为$len\times(cnt+1)$（$+1$表示插入串为空）。最后将未统计的$l=p+1$且$r=q-1$的情况计入答案即可。

使用字符串哈希算法可以简单地实现。

时间复杂度$\mathcal O(n^2\log n)$。

源代码见提交记录。

Offer for Chef

题目大意：

一个长度为$n(n\le10^5)$的数列$A_{1\sim n}$，$q(q\le10)$次询问，每次给出数列$t_{1\sim n}$（$t_i$中只有不超过$50$个数不为$0$）和一个整数$k$，问将这个数列分为$k$段，定义每一段的价值为区间内每个元素$A_i\cdot t_i$之和。总收益为所有区间价值的按位与。最大化总收益。

思路：

原题链接CF981D。

显然我们可以将$A_i\cdot t_i=0$的数去掉，记剩下数的个数为$m$。

从高到低枚举答案的每一个二进制位，判断是否可以为$1$。若可以，则在保留这一位的情况下处理下一位。判定某一位是否能为$1$可以用一个$\mathcal O(m^3)$的动态规划实现，这里不再赘述。

大约枚举$60$个二进制位，时间复杂度$\mathcal O(60\cdot qm^3)$。

源代码见提交记录。

Mininum XOR over Tree

题目大意：

给定一棵$n(n\le2\times10^5)$的有根树，每个结点有权值$w_i(1\le w_i<2^20)$。$q(q\le10^6)$次询问，给定结点$v$和参数$k(q\le k<2^20)$，求对于子树$v$中所有结点$u$，$w_u\oplus k$的最大值，并输出使答案最大的编号最小的$u$。强制在线。

思路：

以DFS序为时间，建立可持久化01字典树。查询时就在子树对应的区间内查找能异或出的最大值。

考虑如何根据这个$w_u\oplus k$的最大值求出最小的$u$。

将所有结点以$w_i$为第一关键字，DFS序为第二关键字排序。维护区间内结点编号的最小值。询问时由于知道了$w_u$，只须在对应权值、对应DFS序的区间内查找最大值即可。这可以用稀疏表方便地实现。

时间复杂度$\mathcal O(n\log n+(n+q)\log w_i)$。

实现上需要注意常数。

源代码见提交记录。