朴素贝叶斯法（naive Bayes algorithm）

对于给定的训练数据集，朴素贝叶斯法首先基于iid假设学习输入/输出的联合分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

一、目标

---

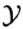设输入空间是n维向量的集合，输出空间为类标记集合= {c₁, c₂, ..., c_k}。X是定义在上的随机变量，Y是定义在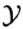上的随机变量。P(X, Y)是X和Y的联合概率分布。训练数据集 T = {(x₁, y₁), (x₂, y₂), ..., (x_N, y_N)}由P(X, Y)独立同分布产生。

朴素贝叶斯法的学习目标是习得联合概率分布P(X, Y)，以此计算后验概率，从而将实例分到后验概率最大的类中。由于P(X, Y) = P(Y)P(X|Y)，因此学习目标可以具体到先验概率分布P(Y = c_k)和条件概率分布P(X = x|Y = c_k)(k = 1, 2, ..., K)。

二、后验概率最大化的原理

---

最大化后验概率等价于最小化期望损失（expected loss），或者说条件风险（conditional risk）。设选择0-1损失函数

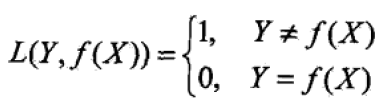
其中f(X)是分类决策函数，则期望损失为

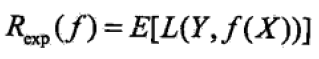
由于期望是对联合分布P(X, Y)取的，因此上式可推出

由贝叶斯判定准则（Bayes decision rule）：最小化总体风险，只需在每个样本上选择那个能使条件风险最小的类别标记。于是

这样一来，根据期望风险最小化准则就得到后验概率从最大化准则：

另一方面，由条件独立性假设

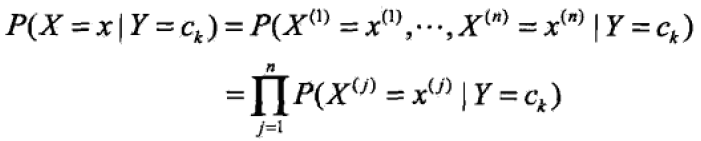
与贝叶斯定理

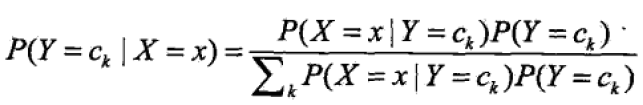
得到

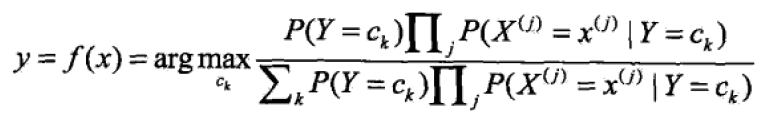
由于上式中分布对c_k都是相同的，因此

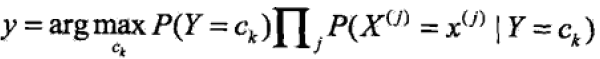
三、参数估计：极大似然估计

---

先验概率P(Y = c_k)的极大似然估计：

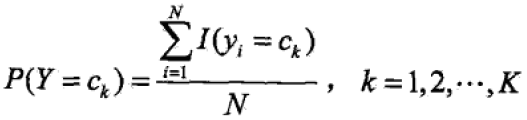
条件概率P(X^(j) = a_jl|Y = c_k)的极大似然估计：

其中设第j个特征x^(j)可能的取值集合为{a_j1, a_j2, ..., a_jSj}，I为指示函数。

四、算法伪码及实现

---

书中给中了算法的伪码

下面给出朴素贝叶斯算法的具体实现

『python』代码摘自https://www.cnblogs.com/yiyezhouming/p/7364688.html

#coding:utf-8
# 极大似然估计  朴素贝叶斯算法
import pandas as pd
import numpy as np

class NaiveBayes(object):
    def getTrainSet(self):
        dataSet = pd.read_csv('C://pythonwork//practice_data//naivebayes_data.csv')
        dataSetNP = np.array(dataSet)  #将数据由dataframe类型转换为数组类型
        trainData = dataSetNP[:,0:dataSetNP.shape[1]-1]   #训练数据x1,x2
        labels = dataSetNP[:,dataSetNP.shape[1]-1]        #训练数据所对应的所属类型Y
        return trainData, labels

    def classify(self, trainData, labels, features):
        #求labels中每个label的先验概率
        labels = list(labels)    #转换为list类型
        P_y = {}       #存入label的概率
        for label in labels:
            P_y[label] = labels.count(label)/float(len(labels))   # p = count(y) / count(Y)

        #求label与feature同时发生的概率
        P_xy = {}
        for y in P_y.keys():
            y_index = [i for i, label in enumerate(labels) if label == y]  # labels中出现y值的所有数值的下标索引
            for j in range(len(features)):      # features[0] 在trainData[:,0]中出现的值的所有下标索引
                x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]]
                xy_count = len(set(x_index) & set(y_index))   # set(x_index)&set(y_index)列出两个表相同的元素
                pkey = str(features[j]) + '*' + str(y)
                P_xy[pkey] = xy_count / float(len(labels))

        #求条件概率
        P = {}
        for y in P_y.keys():
            for x in features:
                pkey = str(x) + '|' + str(y)
                P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y])    #P[X1/Y] = P[X1Y]/P[Y]

        #求[2,'S']所属类别
        F = {}   #[2,'S']属于各个类别的概率
        for y in P_y:
            F[y] = P_y[y]
            for x in features:
                F[y] = F[y]*P[str(x)+'|'+str(y)]     #P[y/X] = P[X/y]*P[y]/P[X]，分母相等，比较分子即可，所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[y]

        features_label = max(F, key=F.get)  #概率最大值对应的类别
        return features_label

if __name__ == '__main__':
    nb = NaiveBayes()
    # 训练数据
    trainData, labels = nb.getTrainSet()
    # x1,x2
    features = [2,'S']
    # 该特征应属于哪一类
    result = nb.classify(trainData, labels, features)
    print features,'属于',result