（二）校园信息通微信小程序从后台获取首页的数据笔记

在从后台获取数据之前，需要先搭建好本地服务器的环境。

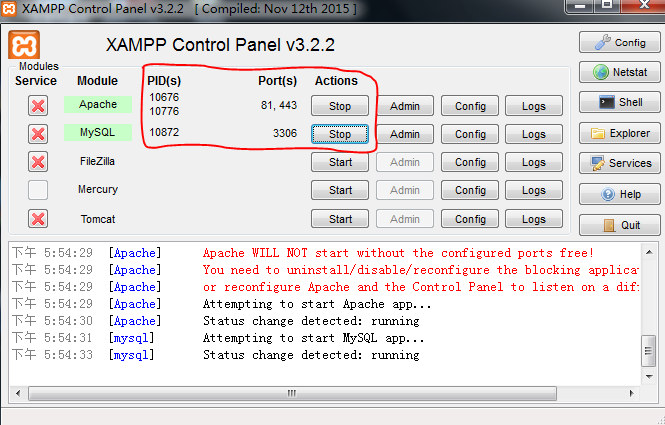
确保Apache,MySql处于开启状态。下图为Apache,MySql处于开启时状态

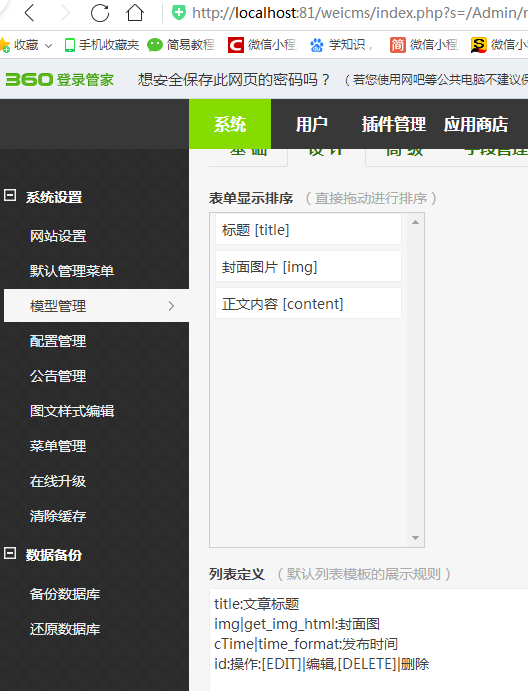
然后进入后台管理平台进行字段和列表的定义

然后在后台添加数据

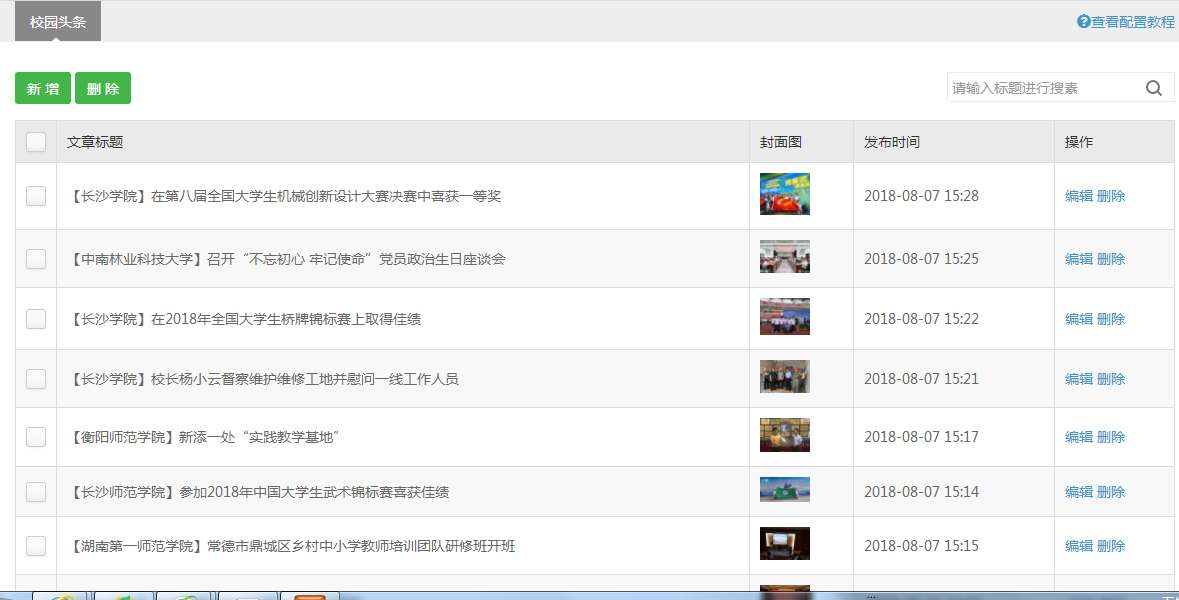
数据添加好后，就开始写接口文件的代码。然后在微信小程序里调用写好的接口就可以获取到刚刚添加的数据了。

接口文件源码如下

class SchoolController extends AddonsController{
    function getList(){
        $list = M('school')->order('id desc')->field('id,title,img,cTime')->select();
        foreach($list as &$vo) {
            $vo['img'] = get_cover_url($vo['img']);
            $vo['cTime'] = time_format($vo['cTime']);
        }
        //dump($list);
        $this->ajaxReturn($list);
    }
｝

接口文件写好后，然后在.js文件里面使用

wx.request(OBJECT)

发起网络请求，在URL参数写入上面写的接口，然后小程序就可以获取到后台的数据了

源码如下：

Page({
  data:{
    newsList:[],
    HomeIndex: 0
  },
  onLoad: function () {
    var that = this;
    wx.request({
      url: 'http://localhost:81/weicms/index.php?s=/addon/School/School/getList',
      data: {},
      header: {
        'content-type': 'application/json'
      },
      success: function (res) {
        wx.setStorage({
          key: 'newsList',
          data: res.data,
        })
        that.setData({
          newsList: res.data
        })
      }
    })
｝)

wx.setStorage({
          key: 'newsList',
          data: res.data,
        })
这是微信小程序的本地缓存。后面再详细说明。
这里先说一下setData

that.setData({
          newsList: res.data
        })

这里实现的是将从服务器获取的数据res.data赋给newsList。
使用

   console.log(res.data)

就可以在控制台看到从后台取过来的数据了。

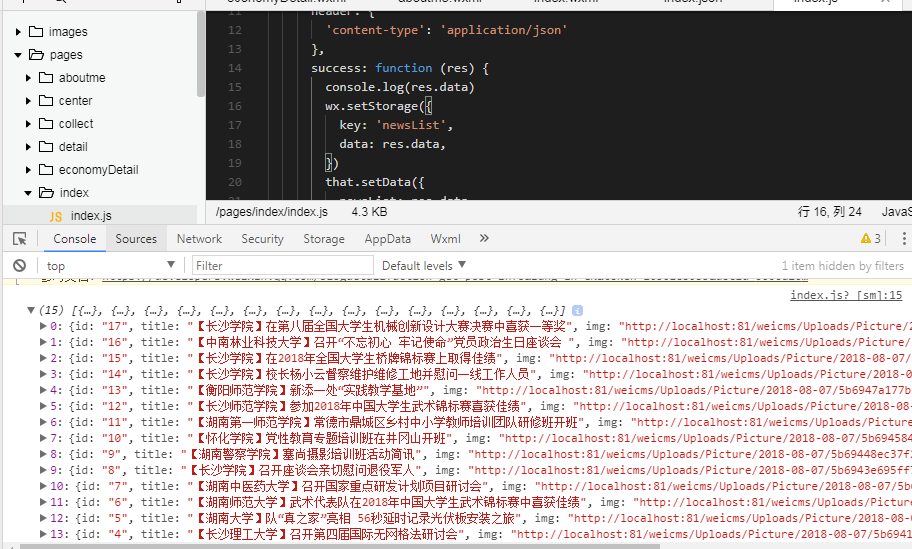
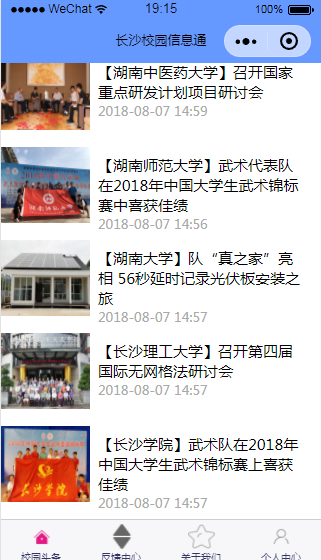
然后在视图层就进行数据绑定，就可以把数据显示在微信小程序的首页了
.wxml文件

<view class="wrap">
  <template name="lists">
    <navigator url='../../pages/detail/detail?id={{id}}' hover-class="navigator-hover">
      <view class='imgs'>
        <image src="{{img}}"  background-size="cover" mode="scaleToFill"></image>
      </view>
      <view class='infos'>
        <view class="title">{{title}}</view>
        <view class="date">{{cTime}}</view>
      </view>
    </navigator>
  </template>
</view>
<view wx:if="{{HomeIndex == 0}}">
<block wx:for="{{newsList}}" wx:key="*this">
  <template is="lists" data="{{...item}}"/>
</block>
</view>

首页显示数据