【ZJOI2017 Round1练习&BZOJ4765】D1T3 普通计算姬（主席树，分块）

题意：

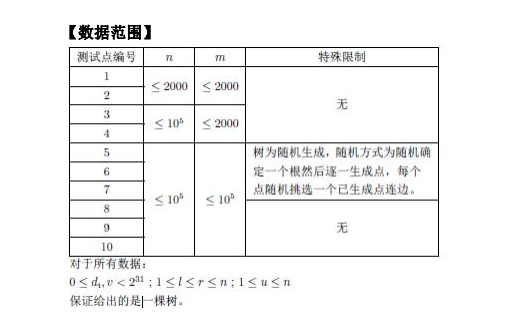
思路：分块

使用树状数组维护sum[i]的前缀和

使用主席树维护root到u的路径上点的编号出现的个数

每次操作如果是修改就加入队列

如果是询问，考虑块内操作对询问的影响，每次在x点加上y会使x到root的点sum都加上y

每根号n次操作就暴力重构一次，清空队列并求出新的sum[i]的前缀和

 var t:array[..]of record
                            l,r:longint;
                            s:int64;
                           end;
     sum,bit:array[..]of int64;
     stk:array[..,..]of longint;
     head,vet,next,fa,a:array[..]of longint;
     root:array[..]of longint;
     n,m,x,y,i,j,top,tot,cnt,kuai,rt,op:longint;
     ans,tmp:int64;
 
 procedure add(a,b:longint);
 begin
  inc(tot);
  next[tot]:=head[a];
  vet[tot]:=b;
  head[a]:=tot;
 end;
 
 procedure pushup(p:longint);
 begin
  t[p].s:=t[t[p].l].s+t[t[p].r].s;
 end;
 
 procedure update(l,r,x:longint;var p:longint);
 var mid:longint;
 begin
  inc(cnt); t[cnt]:=t[p];
  p:=cnt; inc(t[p].s);
  if l=r then exit;
  mid:=(l+r)>>;
  if x<=mid then update(l,mid,x,t[p].l)
   else update(mid+,r,x,t[p].r);
  pushup(p);
 end;
 
 function query(l,r,x,y,p:longint):int64;
 var mid:longint;
 begin
  if (l>=x)and(r<=y) then exit(t[p].s);
  mid:=(l+r)>>;
  query:=;
  if x<=mid then query:=query+query(l,mid,x,y,t[p].l);
  if y>mid then query:=query+query(mid+,r,x,y,t[p].r);
  pushup(p);
 end;
 
 procedure dfs1(u:longint);
 var e,v:longint;
 begin
  root[u]:=root[fa[u]];
  update(,n,u,root[u]);
  e:=head[u];
  while e<> do
  begin
   v:=vet[e];
   if v<>fa[u] then
   begin
    fa[v]:=u;
    dfs1(v);
   end;
   e:=next[e];
  end;
 end;
 
 procedure dfs2(u:longint);
 var e,v:longint;
 begin
  sum[u]:=a[u];
  e:=head[u];
  while e<> do
  begin
   v:=vet[e];
   if v<>fa[u] then
   begin
    dfs2(v);
    sum[u]:=sum[u]+sum[v];
   end;
   e:=next[e];
  end;
 end;
 
 function lowbit(x:longint):longint;
 begin
  exit(x and (-x));
 end;
 
 procedure addbit(x:longint;y:int64);
 begin
  while x<=n do
  begin
   bit[x]:=bit[x]+y;
   x:=x+lowbit(x);
  end;
 end;
 
 function querybit(x,y:longint):int64;
 var k:longint;
 begin
  k:=y;
  querybit:=;
  while k> do
  begin
   querybit:=querybit+bit[k];
   k:=k-lowbit(k);
  end;
  k:=x-;
  while k> do
  begin
   querybit:=querybit-bit[k];
   k:=k-lowbit(k);
  end;
 end;
 
 procedure build;
 var i:longint;
 begin
  for i:= to n do bit[i]:=;
  for i:= to n do addbit(i,sum[i]);
 end;
 
 begin
  assign(input,'common.in'); reset(input);
  assign(output,'common.out'); rewrite(output);
  readln(n,m);
  kuai:=;
  for i:= to n do read(a[i]);
  for i:= to n do
  begin
   readln(x,y);
   if x= then rt:=y
    else
    begin
     add(x,y);
     add(y,x);
    end;
  end;
  dfs1(rt);
  fillchar(head,sizeof(head),);
  tot:=;
  for i:= to n do
   if i<>rt then add(fa[i],i);
  dfs2(rt);
  build;
 
  for i:= to m do
  begin
   readln(op,x,y);
   if op= then
   begin
    inc(top); stk[top,]:=x; stk[top,]:=y-a[x];
    a[x]:=y;
   end
    else
    begin
     ans:=querybit(x,y);
     for j:= to top do
     begin
      tmp:=query(,n,x,y,root[stk[j,]]);
      ans:=ans+stk[j,]*tmp;
     end;
     writeln(ans);
    end;
   if i mod kuai= then
   begin
    top:=;
    dfs2(rt);
    build;
   end;
  end;
  close(input);
  close(output);
 end.