A - Ability Draft Gym - 102155A 状压DP

传送门

题意：有两个队伍，每队有n个人，每个人可以有s个普通技能和一个特殊技能。现在可以按照顺序抽技能卡，问各自都在最优策略下双方队伍的技能总分最大差值。

思路：算是一道看着简单但思路形成比较麻烦的一题。 首先因为贪心有后效性，排除贪心，考虑dp。

发现特殊技能每个人只能有一次，所以想着通过将每个队伍里哪些人选了特殊技能加入dp的状态，这样我们就可以一步知道当前普通技能和特殊技能还剩多少个了。

如当前轮到第pos个人，前面两队一共有x个人选了特殊技能，那么特殊技能就用掉了x个，普通技能用掉了(pos-1)-x个。又因为如果调这两个技能其中给一个的话肯定是挑最大的那个，所以就相当于对一个排序好（从大到小）的两个技能数组从前往后挑。

那么怎么记录每个队伍哪些人用了特殊技能呢？因为我们将这个状态要放进dp数组里，所以我们想用一个数字就能表示上述的状态。

这个时候就用到状态压缩。

因为每个队伍的人数不超过五个人，我就用二进制下的

[00000,11111]的数表示每个队伍里面每一个人是否用了大招的情况，0代表这一位人没用，1代表用了。这样对应十进制下，我们只需要一个32大小的数组来存储这个状态即可。

然后对于状态转移，因为我们想让两队分差尽量大（采用记忆化搜索）：

1.如果当前轮到的人是一队的，那么他产生的值对答案来说是一个正贡献，选DP最大的作为转移。 转移方程为

\(dp[i][j][k] = max(DP(pos+1,sta1|(1<<order[pos]) , sta2) + special[id2], DP(pos+1,sta1,sta2)+ normal[id1])\)

表示当前选或不选特殊技能的最优解，选了的话sta1集合加入这一位的贡献。

2.如果当前轮到的人是二队的，那么他产生的值对答案来说是一个负贡献，选DP最小的作为转移，转移方程为

\(dp[i][j][k] = min(DP(pos+1,sta1 , sta2|(1<<order[pos])) - special[id2], DP(pos+1,sta1,sta2) - normal[id1] )\)

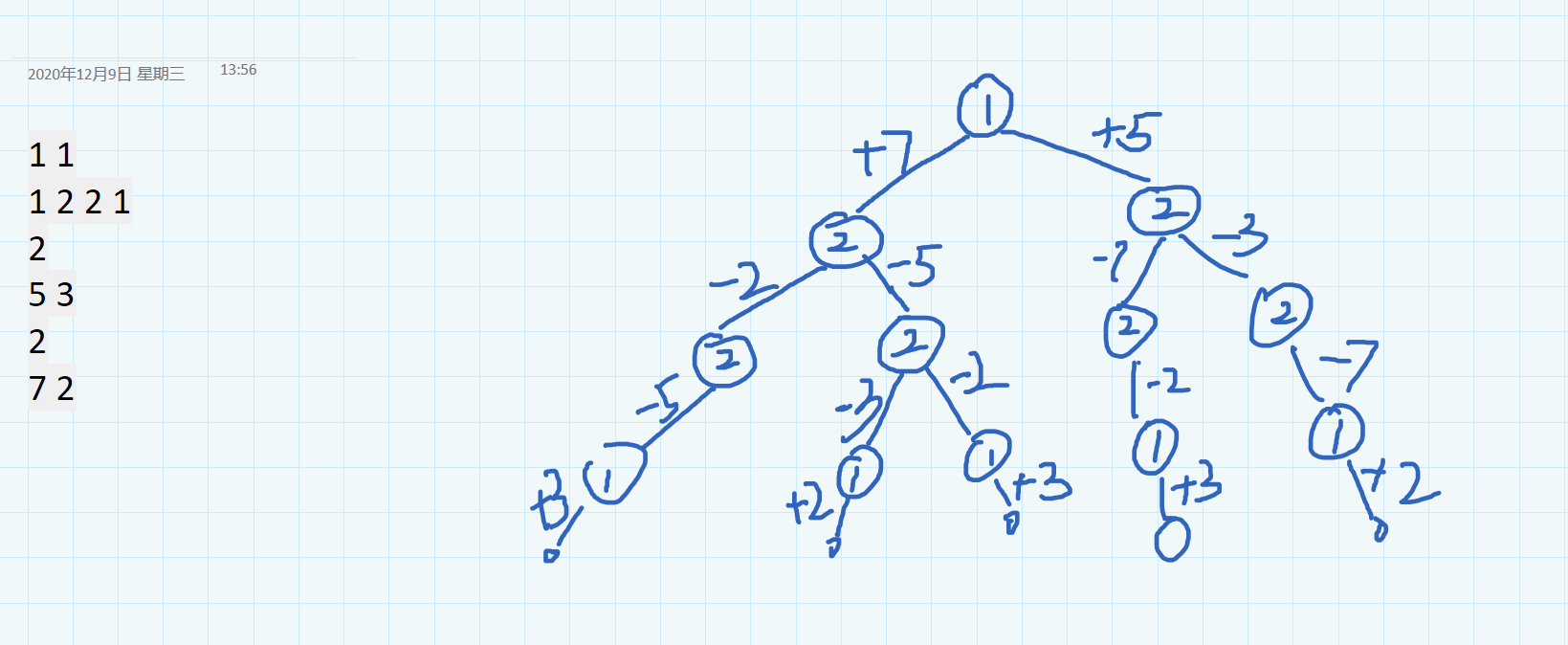
通过第一个样例画出本方法的递归树如下图，方便读者理解：

AC代码如下：

view code

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include <queue>
#include<sstream>
#include <stack>
#include <set>
#include <bitset>
#include<vector>
#define FAST ios::sync_with_stdio(false)
#define abs(a) ((a)>=0?(a):-(a))
#define sz(x) ((int)(x).size())
#define all(x) (x).begin(),(x).end()
#define mem(a,b) memset(a,b,sizeof(a))
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define rep(i,a,n) for(int i=a;i<=n;++i)
#define per(i,n,a) for(int i=n;i>=a;--i)
#define endl '\n'
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef pair<ll,ll> PII;
const int maxn = 1e5+200;
const int inf=0x3f3f3f3f;
const double eps = 1e-7;
const double pi=acos(-1.0);
const int mod = 1e9+7;
inline int lowbit(int x){return x&(-x);}
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
void ex_gcd(ll a,ll b,ll &d,ll &x,ll &y){if(!b){d=a,x=1,y=0;}else{ex_gcd(b,a%b,d,y,x);y-=x*(a/b);}}//x=(x%(b/d)+(b/d))%(b/d);
inline ll qpow(ll a,ll b,ll MOD=mod){ll res=1;a%=MOD;while(b>0){if(b&1)res=res*a%MOD;a=a*a%MOD;b>>=1;}return res;}
inline ll inv(ll x,ll p){return qpow(x,p-2,p);}
inline ll Jos(ll n,ll k,ll s=1){ll res=0;rep(i,1,n+1) res=(res+k)%i;return (res+s)%n;}
inline int read(){ int f = 1; int x = 0;char ch = getchar();while(ch>'9'||ch<'0') {if(ch=='-') f=-1; ch = getchar();}while(ch>='0'&&ch<='9') x = (x<<3) + (x<<1) + ch - '0',  ch = getchar();return x*f; }
int dir[4][2] = { {1,0}, {-1,0},{0,1},{0,-1} };

int normal[50];     //normal数组表示普通技能
int special[50];    // 特殊技能
int order[50];  // 题目的抽卡顺序
ll dp[50][100][100];    // dp[i][j][k]表示， 轮到第i个人抽卡时，且此时1队抽卡情况为j（二进制下第x位表示这个是否有抽特殊技能），k同理表示二队
int p1;     //两个技能的数组大小
int p2;

int n,s;

int Status(int x)       //判断用了目前状态有多少人用了大招
{
    int sum = 0;
    while(x)
    {
        sum += x&1;
        x >>= 1;
    }
    return sum;
}

bool check(int pos)     //看一下自己往后有没有抽卡机会
{
    rep(i,pos+1, 2*n*(s+1)) if(order[i]==order[pos])
    {
        return true;
    }
    return false;
}

int Flag(int pos)       //看一下是哪个队
{
    if(order[pos]<=n) return 1;
    return -1;
}

ll DP(int pos, int sta1, int sta2)
{
    if(pos>n*2*(s+1)) return 0;
    if(dp[pos][sta1][sta2] != -1) return dp[pos][sta1][sta2];
    int use = Status(sta1) + Status(sta2);  //看看目前有多少人用了大招
    int id2 = use + 1;  //那么目前会调的大招下标为id2
    int id1 = pos - use;    //普通技能被调到第id1个
    ll tmp = 0;
    if(order[pos]<=n)       //一队
    {
         int flag = check(pos);     //看看这个人后面有无抽卡机会
         if(!flag&& !( (sta1>>order[pos])&1) )  //如果这是他最后一次抽卡且还没抽大招，那赶紧抽大招
         {
             tmp = DP(pos+1,sta1|(1<<order[pos]) , sta2) + special[id2]*Flag(pos);
         }
         else if(!( (sta1>>order[pos])&1))  //如果不是最后一个人，而且没抽大招，那就有两种选择，选最大的
         tmp = max(DP(pos+1,sta1|(1<<order[pos]) , sta2) + special[id2]*Flag(pos), DP(pos+1,sta1,sta2)+ normal[id1] *Flag(pos) );
         else   //如果选了大招，就老老实实挑普通技能
         tmp = DP(pos+1,sta1,sta2) + normal[id1]*Flag(pos);
         return dp[pos][sta1][sta2] = tmp;
    }
    //二队同理，换成每步取最小即可。
     int flag = check(pos);
     int sysbom = Flag(pos);
     order[pos] -= n;

     if(!flag&& !( (sta2>>order[pos])&1) )
     {
         tmp = DP(pos+1,sta1 , sta2|(1<<order[pos]))  + special[id2]*sysbom;
     }
     else if(!( (sta2>>order[pos])&1))
     tmp = min(DP(pos+1,sta1 , sta2|(1<<order[pos]))   + special[id2]*sysbom, DP(pos+1,sta1,sta2)   + normal[id1]*sysbom );
     else
     {
         tmp = DP(pos+1,sta1,sta2)   + normal[id1]*sysbom;
     }
    order[pos] += n;
     return dp[pos][sta1][sta2] = tmp;
}

int main()
{
    n = read(), s = read();
    rep(i,1,n*2*(s+1)) order[i] = read();
    p1 = read(); rep(i,1,p1) normal[i] = read();
    p2 = read(); rep(i,1,p2) special[i] = read();
    sort(normal+1,normal+1+p1, greater<int>()); //从大到小对技能排序
    sort(special+1,special+1+p2, greater<int>());
    mem(dp,-1);
    cout<<DP(1,0,0)<<endl;
    return 0;
}