在matlab中使用遗传算法执行最优化
遗传算法是一种通用的最优化方法,具体原理可以看:遗传算法详解与实验。下面记录在Matlab中如何使用遗传算法来做优化。
用法
调用方式如下:
1 x = ga(fun,nvars)
2 x = ga(fun,nvars,A,b)
3 x = ga(fun,nvars,A,b,Aeq,beq)
4 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)
5 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)
6 x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)
7 x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon)
8 x = ga(fun,nvars,A,b,[],[],lb,ub,nonlcon,IntCon,options)
9 x = ga(problem)
10 [x,fval] = ga(___)
11 [x,fval,exitflag,output] = ga(___)
12 [x,fval,exitflag,output,population,scores] = ga(___)
参数解释
fun: 要执行最优化的函数,用于输入待优化变量$x$。只能包含一个参数,可以是单个标量,也可以是向量。输出一个标量。
nvars: 最优化函数传入向量的元素数量。
A, b: 线性不等式约束的系数。即待优化变量$x$要满足$A\cdot x \le b$。
Aeq, beq: 线性等式约束的系数。即待优化变量$x$要满足$Aeq\cdot x = beq$。
lb, ub: 传入向量的取值范围。即待优化变量$x$要满足$lb\le x\le ub$。
nonlcon: 定义非线性不等式约束和等式约束的函数。该函数只能包含一个参数用于接受待优化变量$x$,然后输出不等式约束值$C(x)$和等式约束值$Ceq(x)$。约束$x$满足$C(x)\le 0$和$Ceq(x)=0$。
IntCon: 限制待优化参数为整数,传入需要限制为整数的待优化参数的位置。如对于3维变量$x$,设置IntCon为$[1,3]$表示第一和第三维的元素被限制为整数。
options: 遗传算法的设置,设置初始化、迭代次数、种群大小等。具体请看链接。
[]: 对于不想使用的约束,可以用中括号[]省略。
传出参数
x: 最优化后的变量。
fval: $x$对应的函数值。
exitflag: 遗传算法结束标志,一个整数。分别解释如下:

output: 遗传算法的优化过程信息。
population: 遗传迭代最后的种群。数组每行表示一个函数变量。
scores: 最后种群的个体值。也就是数组中各个变量的函数值。
例子
首先定义待优化函数:
1 function outp = func(varargin)
2 narginchk(1,2);
3 if nargin == 1
4 x = varargin{1}(1);
5 y = varargin{1}(2);
6 elseif nargin == 2
7 x = varargin{1};
8 y = varargin{2};
9 end
10 outp = 2*exp((-(x+3).^2-(y-3).^2)/10) + 1.2*exp((-(x-3).^2-(y+3).^2)/10) + exp(-cos(3*x)-sin(3*y));
11 outp = -outp;
12 end
然后是该函数的可视化和优化:
1 %% 函数可视化
2 x = linspace(-5,0,500);
3 y = linspace(0,5,500);
4 [X, Y] = meshgrid(x, y);
5
6 Z = func(X, Y);
7 mesh (X,Y,Z);
8
9 %% 优化
10 [x, f] = ga(@func, 2);
通过可视化可以看到最小值大概在$(-3.14, 3.66)$附近:
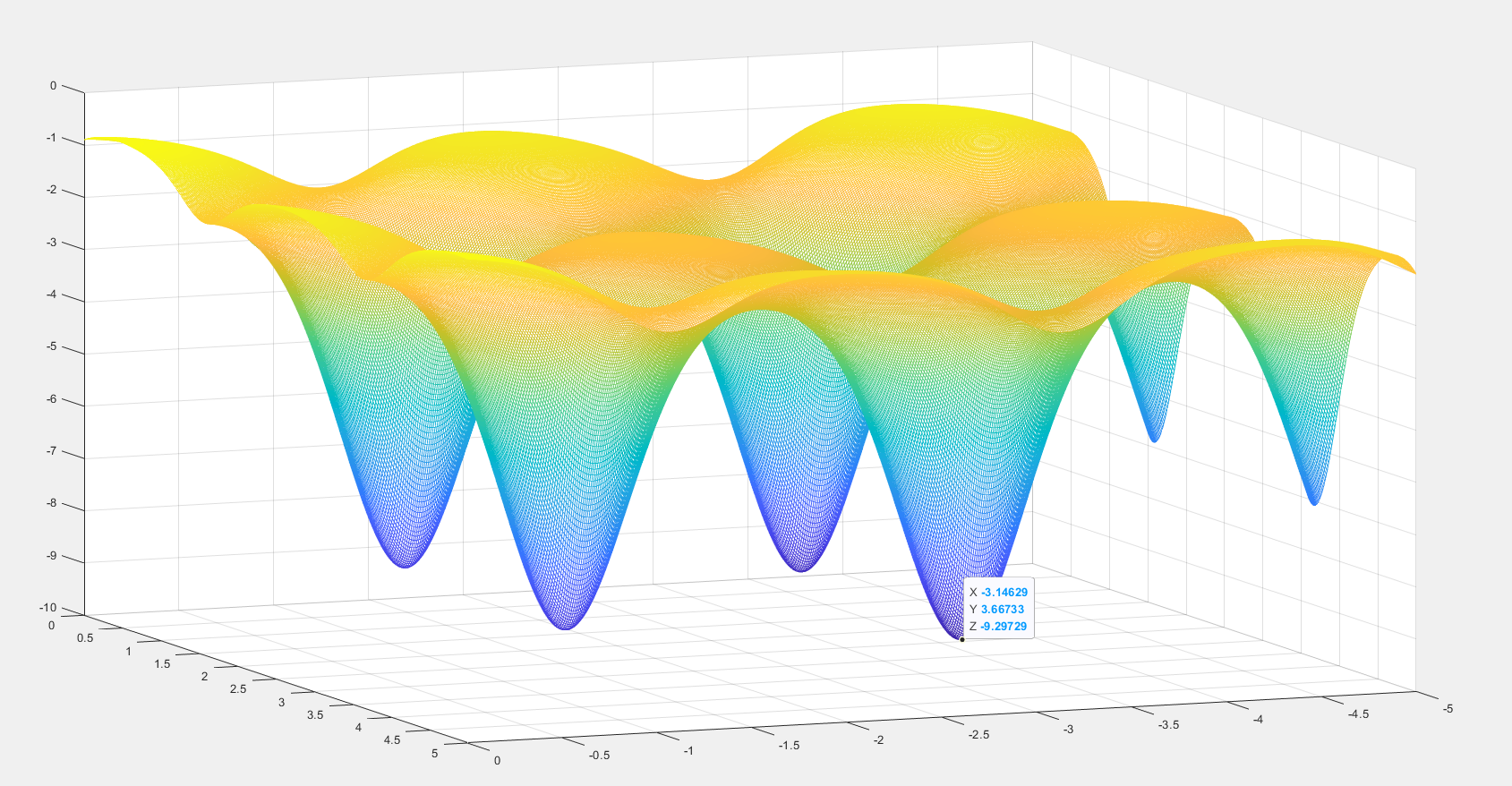
优化结果也是如此:
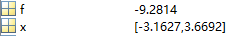
在matlab中使用遗传算法执行最优化的更多相关文章
- Matlab中的一些小技巧
(转于它处,仅供参考) 1.. Ctrl+C 中断正在执行的操作 如果程序不小心进入死循环,或者计算时间太长,可以在命令窗口中使用Ctrl+c来中断.MATLAB这时可能正疲于应付,响应会有些滞后. ...
- 【matlab】将matlab中数据输出保存为txt或dat格式
将matlab中数据输出保存为txt或dat格式 总结网上各大论坛,主要有三种方法. 第一种方法:save(最简单基本的) 具体的命令是:用save *.txt -ascii x x为变量 *.txt ...
- 在matlab中配置vlfeat
[转自]http://cnyubin.com/?p=85 在VLFeat官网上是这么介绍VLFeat的:VLFeat开源库实现了很多著名的机器视觉算法,如HOG, SIFT, MSER, k-mean ...
- matlab中subplot函数的功能
转载自http://wenku.baidu.com/link?url=UkbSbQd3cxpT7sFrDw7_BO8zJDCUvPKrmsrbITk-7n7fP8g0Vhvq3QTC0DrwwrXfa ...
- 将matlab中数据输出保存为txt或dat格式
:FID= FOPEN(filename,permission) 用指定的方式打开文件 FID=+N(N是正整数):表示文件打开成功,文件代号是N. FID=-1 : 表示文件打 ...
- Matlab中reshape函数的使用
reshape把指定的矩阵改变形状,但是元素个数不变, 例如,行向量: a = [1 2 3 4 5 6] 执行下面语句把它变成3行2列: b = reshape(a,3,2) 执行结果: b = 1 ...
- Matlab中的数据类型
Matlab中有15种基本数据类型,主要是整型.浮点.逻辑.字符.日期和时间.结构数组.单元格数组以及函数句柄等. 1.整型:(int8:uint8:int16:uint16:int3 ...
- 关于MATLAB中的tic toc的问题
关于MATLAB中的tic toc的问题 其一) MATLAB实际单位时间计时函数的具体应用,在编写程序时,经常需要获知代码的执行实际时间,这就需要在程序中用到计时函数,matlab中提供了以下三种方 ...
- MATLAB中的函数的归总
字符串操作函数 1. 函数eval可以用来执行用字符串表示的表达式 2. 函数deblank可以去掉字符串末尾的所有空格 3. 函数findstr可以用来在长 ...
- MATLAB中多行注释的三种方法
MATLAB中多行注释的三种方法 A. %{ 若干语句 %} B. 多行注释: 选中要注释的若干语句, 编辑器菜单Text->Comment, 或者快捷键Ctrl+R 取消注释: 选中要取消注释 ...
随机推荐
- 【测试平台开发】——02Vue前端框架实战—router路由设计(登录页面)
一.安装vue-cli Mac系统: sudo npm install -g vue-cli 检查是否安装好: vue -V 二.创建新项目 1.打开Vue项目管理器 输入命令: vue ui 但是没 ...
- CSS – Variables
参考: Youtube – CSS Variables - CSS vs Sass - variables inside media queries Why we prefer CSS Custom ...
- Figma 学习笔记 – Image
参考: Figma Tutorial: Images 3 Ways to Insert Image 1. rectangle / frame + fill 画一个 rectangle / frame ...
- SQL Server – 冷知识 (新手)
前言 没有系统化学一本语言或技术, 那便会被一些冷知识坑. 这里做些记入. 变量作用域 SQL 是远古语法, 声明变量在最顶部就是一条上古法则. 如果我看见有了用这个法则写 C# 或 JS 我就会杀了 ...
- 前端基本功——面试必问系列(1):都2024了,还没吃透Promise?一文搞懂
写在前面: 大家好,我是山里看瓜,该系列文章是为了帮助大家不管面试还是开发对前端的一些基本但是很重要的知识点认识更加深入和全面. 想写这个系列文章的初衷是:我发现前端的很多基本知识,使用起来很简单,定 ...
- Spring —— IoC入门案例
IoC入门案例 思路分析: 1.管理什么?(Service与Dao) 2.如何将被管理的对象告知IoC容器?(配置) 3.被管理的对象交给IoC容器,如何获取到IoC容器? ...
- 深入理解 Nuxt.js 中的 app:error:cleared 钩子
title: 深入理解 Nuxt.js 中的 app:error:cleared 钩子 date: 2024/9/28 updated: 2024/9/28 author: cmdragon exce ...
- crypt.h:No such file or directory 报错处理
crypt.h:No such file or directory 报错处理 前言:本文初编辑于2024年9月28日 CSDN主页:https://blog.csdn.net/rvdgdsva 博客园 ...
- nestjs 和 .net DI 使用并注册的区别
核心:对象之间的关系 各种 引用 --- 方便使用各种服务 1. .net 注册服务 三种注册方式 build.Service.Addsigtel 单例 瞬时 等 .addSingtel<IU ...
- 云原生周刊:K8s 中的服务和网络 | 2024.4.29
开源项目推荐 k8s-image-swapper k8s-image-swapper 是 Kubernetes 的一个变更 Webhook,它将镜像下载到自己的镜像仓库,并将镜像指向该新位置.它是 d ...
