hot100之二分查找

搜索插入位置(035)

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int lef = -1;
        int rig = n;
        while(lef+1 < rig){
            int mid = (lef + rig) / 2;
            if (nums[mid] < target){
                lef = mid;
            }else rig = mid;
        }
        return rig;
    }
}

• 分析

基础二分

搜索二维矩阵(074)

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int lef = -1;
        int rig = m*n;
        while (lef+1 < rig){
            int mid = (lef + rig) / 2;
            int x = matrix[mid/n][mid%n];

            if (x < target) lef = mid;
            else if (x > target) rig = mid;
            else return true;
        }
        return false;
    }
}

• 分析

把每一个row 横向相连, 作二分

在排序数组中查找元素的第一个和最后一个位置(034)

class Solution {
    public int[] searchRange(int[] nums, int target) {

        int start = searchLower(-1 ,nums, target);
        if (start == nums.length || nums[start] != target) return new int[]{-1,-1};

        int end = searchLower(start, nums, target+1) -1;
        return new int[] {start, end};
    }

    private int searchLower(int lef, int[] nums, int target){

        int rig = nums.length;

        while (lef + 1 < rig){
            int mid = (lef + rig) / 2;
            if (nums[mid] < target) lef = mid;
            else rig = mid;
        }

        return rig;
    }
}

• 分析

通过两次二分 查找 target 和target+1的起始位置, 确定target的范围

搜索旋转排序数组(033)

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length -1;
        int lef = -1;
        int rig = n;
        while (lef + 1< rig){
            int mid = (lef + rig) / 2;
            if (check(nums, target, mid)){       //target在mid右侧
                lef = mid;
            }else rig = mid;
        }
        return nums[rig] == target ? rig : -1;
    }

    private boolean check(int[] nums, int target, int idx){
        int x = nums[idx];
        int end = nums[nums.length-1];

        if (x < end){
            return x < target && target <= end;  // mid在小端 且比target小
        }
        // mid在大端 且< target在小端 || target > mid >
        return x < target || target <= end;
    }
}

• 分析

通过mid和end值的对比, 确定mid的位置<旋转小端, 旋转大端>

根据 mid的位置再分类讨论

寻找旋转排序数组的最小值(153)

class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int lef = -1;
        int rig = n;
        while (lef+1 < rig){
            int mid = (lef + rig) / 2;
            if(nums[mid] > nums[n-1]){   // 在右侧
                lef = mid;
            }else rig = mid;
        }
        return nums[rig];
    }
}

• 分析

判断 mid 在<大端, 小端> →<右移, 左移>

• 感悟

二分用来查找数据的拐点, 以<条件>作check()

寻找两个正序数组的中位数(004)

这题给我写晕厥了

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length){
            return findMedianSortedArrays(nums2, nums1);
        }

        int m = nums1.length;
        int n = nums2.length;

        int lef = -1;
        int rig = m;

        while (lef+1 < rig){
            int mid_nums1 = (lef+rig) / 2;
            int mid_nums2 = (m+n+1) / 2 - (mid_nums1+1) -1;
            if(nums1[mid_nums1] - nums2[mid_nums2+1] <= 0){
                lef = mid_nums1;
            }else rig = mid_nums1;
        }

        int idx_nums1 = lef;
        int idx_nums2 = (m+n+1)/2 - (lef+1) - 1;
        int lef_max_nums1 = idx_nums1 >= 0 ? nums1[idx_nums1] : Integer.MIN_VALUE;
        int lef_max_nums2 = idx_nums2 >= 0 ? nums2[idx_nums2] : Integer.MIN_VALUE;
        int rig_min_nums1 = idx_nums1 + 1 < m ? nums1[idx_nums1+1] : Integer.MAX_VALUE;
        int rig_min_nums2 = idx_nums2 + 1 < n ? nums2[idx_nums2+1] : Integer.MAX_VALUE;

        int max = Math.max(lef_max_nums1, lef_max_nums2);
        int min = Math.min(rig_min_nums1, rig_min_nums2);

        return (m+n)%2 != 0 ? max : (max+min) / 2.0;
    }
}

• 分析

我们取两数组<红>作为总数据集<中位数左侧>的小端, <蓝>作为总数据集<中位数右侧>的大端

假设在<红>全落在第一组

从<红>取出值放入<蓝>

从<蓝>取出值放入<红>

直到<红>全落在第二组

我们可以看到, <红>的sum是先变小, 再变大, 显然我们可以观察到拐点, 即为sum最小值,也是我们要找的数据集小端

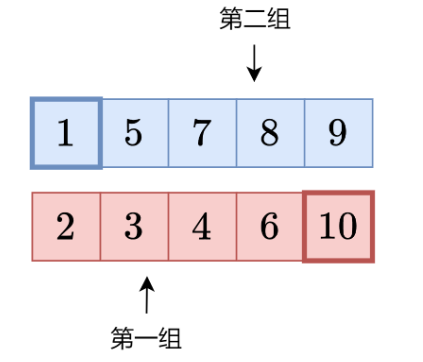
接下来我们通过二分找拐点if(nums1[mid_nums1] - nums2[mid_nums2+1] <= 0)

如果从<红>中取<蓝>对<红>产生正反馈(变大) 取 rig = mid

产生负反馈(变小或不变) 取 lef = mid