Luogu P7503 「HMOI R1」文化课

题传

先想一个巨 shaber 的暴力 DP：设 \(f_{i}\) 为对前 \(i\) 个人分段的最优解，则：

\[f_{i}=\max_{0\le j<i}\{f_{j}+\operatorname{W}(j+1, i)\}
\]

其中：

\[\operatorname{W}(x, y)=\sum_{i=x}^y [l_i \le \max(x_j|j\in [x, y]) \le r_i]
\]

暴力做显然是 \((n^2)\) 的，考虑优化。

如果考虑将决策中的 \(i\) 右移一位，用线段树维护 \(val_i(x)=f_{x-1}+\operatorname{W}(x, i)\) 的话，发现右移时无法快速修改有变化的位置（类似 \(+1\ 0\ 0\ +1\dots\) 状物，不好维护）。

正难则反，考虑某个 \(j\) 会对哪些决策位置 \((x, i)\) 有贡献。

我们将判断条件 \(\max(x_p | p \in [x, i])\) 拆成两部分： \(\max(x_p | p \in [x, j])\) 和 \(\max(x_p | p \in [j, i])\)。

不难画出下图：

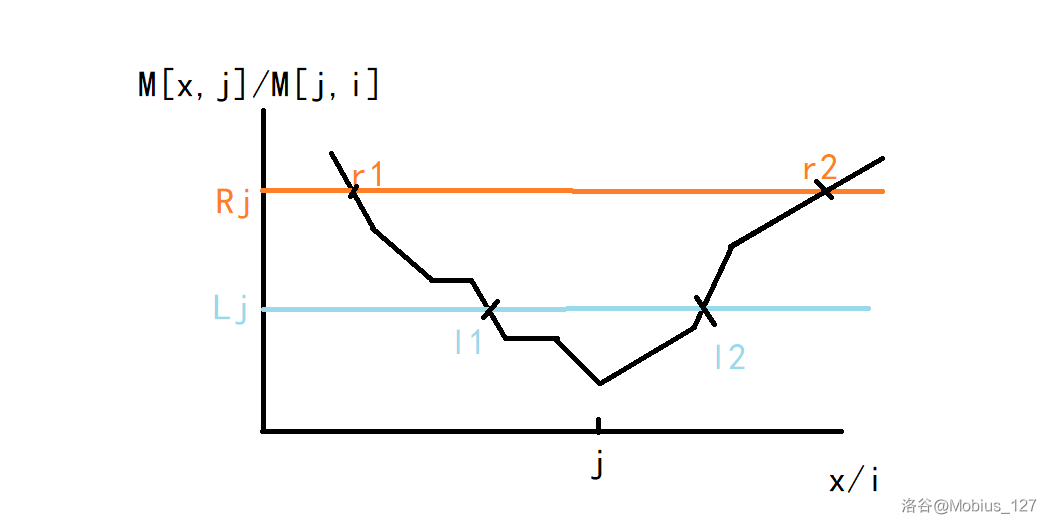
先考虑 \(i\in [l2, r2]\)，对于这一段位置，\(i\) 已经满足了 \(l_j \le \max(x_p | p \in [j, i]) \le r_j\)，那么 \(x\) 只要在 \([R_j, j]\) 之间即可。

然后是 \(i\in [j, l2)\)，此时 \(x\) 就必须满足 \(l_j \le \max(x_p | p \in [x, j]) \le r_j\)，即 \(x \in [r1, l1]\)。

对于 \(i > r2\)，显然 \(j\) 已经贡献不到了。

然后你就发现每个 \(j\) 贡献到的 \(i\) 是连续的，而且对于每个被贡献到的 \(i\)，函数 \(\operatorname{W}\) 区间左端点 \(x\) 也是连续的。

所以我们在 \(j\) 处塞一个 \([r1, l1]\) 区间 +1 的操作，在 \(l2\) 处塞一个 \((l1, j]\) 区间 +1 的操作（\([r1, l1]\) 在前面已经被加过一次了）。

然后在 \(r2+1\) 的位置塞一个消除贡献的区间 -1 操作即可。

操作数显然是 \(O(n)\) 的，\(l1, l2, r1, r2\) 可以单调栈后二分找。

总复杂度 \(O(n\log n)\)。

Code

#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <cctype>
#include <vector>
#define st first
#define nd second
using namespace std;
typedef long long ll;
typedef pair <int, int> Pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
inline int read(){
	char ch=getchar();int x=0, f=1;
	while(!isdigit(ch)){if(ch=='-') f=-1; ch=getchar();}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'), x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
inline int ksm(int a, int b){
	int ret=1;
	for(; b; b>>=1, a=1ll*a*a%mo)
		if(b&1) ret=1ll*ret*a%mo;
	return ret;
}
const int N=1e5+5;
namespace Segment{
	#define ls k<<1
	#define rs k<<1|1
	#define mid (l+r>>1)
	int Mx[N*4], tag[N*4];
	void build(){
		memset(Mx, -9, sizeof(Mx));
		memset(tag, 0, sizeof(tag));
	}
	void upd(int k, int v){Mx[k]+=v, tag[k]+=v;}
	void pushdown(int k){if(tag[k]) upd(ls, tag[k]), upd(rs, tag[k]), tag[k]=0;}
	void pushup(int k){Mx[k]=max(Mx[ls], Mx[rs]);}
	void change(int k, int l, int r, int x, int v){
		if(l==r) return (void)(Mx[k]=max(Mx[k], v));pushdown(k);
		if(x<=mid) change(ls, l, mid, x, v);
		else change(rs, mid+1, r, x, v);
		pushup(k);
	}
	void modify(int k, int l, int r, int x, int y, int v){
		if(x>y) return ;//if(k==1) printf("make %d %d %d\n", x, y, v);
		if(x<=l&&r<=y) return upd(k, v);pushdown(k);
		if(x<=mid) modify(ls, l, mid, x, y, v);
		if(mid<y) modify(rs, mid+1, r, x, y, v);
		pushup(k);
	}
	#undef ls
	#undef rs
	#undef mid
}
int n, a[N], la[N], ra[N], f[N];
Pii L[N], R[N];
vector < pair<Pii, int> > op[N];
int sta[N], top=0;
int find(int x){
	int l=1, r=top, ans=0;
	while(l<=r){
		int mid=l+r>>1;
		if(a[sta[mid]]>=x) l=mid+1, ans=mid;
		else r=mid-1;
	}
	return sta[ans];
}
signed main(){
	n=read();
	for(int i=1; i<=n; ++i) a[i]=read();
	for(int i=1; i<=n; ++i) la[i]=read(), ra[i]=read();
	top=0;
	for(int i=1; i<=n; ++i){
		while(top&&a[sta[top]]<a[i]) --top;
		sta[++top]=i;L[i]=make_pair(find(la[i]), find(ra[i]+1)+1);
	}
	sta[top=0]=n+1;
	for(int i=n; i>=1; --i){
		while(top&&a[sta[top]]<a[i]) --top;
		sta[++top]=i;R[i]=make_pair(find(la[i]), find(ra[i]+1));
		// printf("(%d %d)\n", R[i].first, R[i].second-1);
	}
	for(int i=1; i<=n; ++i)
		if(a[i]<=ra[i])
			op[i].push_back(make_pair((Pii){L[i].nd, L[i].st}, 1)),
			op[R[i].st].push_back(make_pair((Pii){L[i].st+1, i}, 1)),
			op[R[i].nd].push_back(make_pair((Pii){L[i].nd, i}, -1));
	int ans=0;Segment :: build();
	for(int i=1; i<=n; ++i){
		// printf("for %d\n", i);
		Segment :: change(1, 1, n, i, f[i-1]);
		for(auto x : op[i])
			Segment :: modify(1, 1, n, x.st.st, x.st.nd, x.nd);
		f[i]=Segment :: Mx[1];
		// printf("find %d\n", f[i]);
		ans=max(f[i], ans);
	}
	printf("%d\n", ans);
	return 0;
}