SciTech-Mathmatics-Proba. & Stats.: $\large y=ax^2 + bx + c$(非常重要的 抛物线函数) + $\large 高斯分布(正态分布)的Bell Curve钟形曲线 的 pdf(概率分密度曲线方程) 与 cdf(累积分布函数:积分面$积)

SciTech-Mathmatics-Proba. & Stats.: \(\largey=ax^2 + bx + c\)(非常重要的 抛物线函数) + \(\large 高斯分布(正态分布)的Bell Curve钟形曲线 的 pdf(概率密度曲线方程) 与 cdf(累积分布函数:积分面积)\)

Abbreviation

AUC(Area Under Curve): 曲线下面积

VUC(Volume Under Contour): 曲面下体积

\(\large y=ax^2 + bx + c\)(特别重要的函数)

\(\large y = ax^2 + bx + c\) 是 “一维”向“二维(甚至多维)”扩展的“函数”:

• "一维"的"线性函数" 代表与起源 是“Newton的经典力学(作用力、速度、加速度)”: $\large s = s_0 + vt $ 与 \(\large v = v_0 + kt\) 与
• 因为“抛物线”是"物体"在"正交(垂直、水平)的两个方向(维度)"同时受到“力(变量/输入)作用”时的“合成与分解”:
  • 分解维 \(\large x(水平)轴\)上受"一合力(变量/维度)\(\large F_x\)"作“线性(匀速)运动”:
    
    \(\large x = v_0 t + x_0\)
  • 分解维 \(\large y(水平)轴\)上受"一重力(变量/维度)\(\large F_y\)作“匀加速运动”:
    
    \(\large v = gt + v_0,\ h = \dfrac{1}{2} g t^2,\ g=9.8m/s^2\)
  • 合成维 \(\large x, y 正交两轴上\) :
    
    "力"的"分解与合成": “平行四边形(三角函数之余弦)法则”
  • "vector"的"Inner Product(内积)": \(\large a \cdot b = |a| \times |b| \times cos(a \angle b)\)
    
    正是"力的分解与合成(余弦法则、平行四边形法则)"在"高维空间"的推广。

\(\large Measurement\)、\(\large \text{Circle } VS \text{ Relation}\)、\(\large \angle(\text{Angle})\ \text{Measure}\) 与 \(\large \pi\) 如此美丽:

\(\large \text{Circle } VS \text{ Relation}\)、\(\large \angle(\text{Angle})\ \text{Measure}\) 与 \(\large \pi\) 是如此的美丽:

• 当\(\large a 与 b\)"两vector 正交(不相关)"时, \(\large a \angle b =\dfrac{\pi}{2}, \ cos(a \angle b)=0\),
• 当\(\large a 与 b\)"两vector 相关(不正交)"时, \(\large a \angle b \neq \dfrac{\pi}{2}, |\ cos(a \angle b)| \in (0,1]\),
  • $\large a \angle b $的大小(弧度制)，能 \(\large Measure\) 出 \(\large \text{ Strength of Relation }\),
    
    并且函数\(\large f(a, b)=|cos(a \angle b)|\) 使其值 \(\large Normalize到(0,1]\).
  • 函数\(\large s(a, b)= Sign(a \angle b)\)用 "\(\large \text{ positive or negative angle }\)" 映射为
    
    "\(\large a 与 b\)"两vector 相关(不正交)"的"\(\large \text{ positive or negative correlation}\).
• "vector"的"Inner Product(内积)": \(\large a \cdot b = |a| \times |b| \times cos(a \angle b)\)
  
  则"扩展"到"\(\large K^n(即\text{ n }维 \text{ K数域上 Vector Space }) 的任意两个\text{ vector }: a\ and \ b\),
  
  且用\(\large 模长 |a|\)去"\(\large Measure\)"所有\(\large \text{ n }维\text{ Variables }\)的"Total Attribution(总作用)".
• 点积、叉积、内积、外积【汇总对比】

高斯分布(正态分布)的Bell Curve钟形曲线

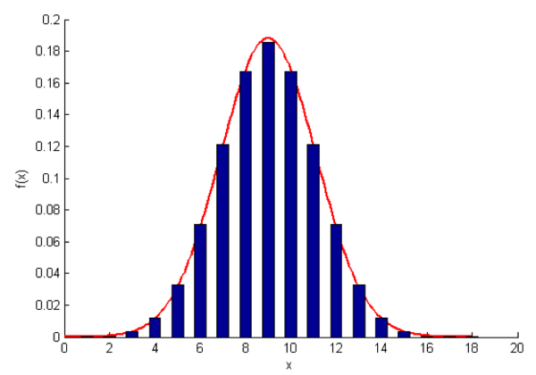
参考“正态分布”，完整的看完看懂，则收获巨大。

Normal distribution(正态分布) 又称为“常态分布”或 Gaussian distribution(高斯分布)，

通常记作:

\[\large X \sim N(\mu, \sigma^2)
\]

• \(\mu\) 是“正态分布”的“数学期望(均值)”,
• \(\sigma^2\) 是“正态分布”的“方差”。
• “标准正态分布”: \(\mu = 0, \ \sigma = 1\) 的“正态分布”。
  
  "标准正态分布" 重要的原因之一是 "任意的正态分布"的"计算"很都容易转化为"标准正态分布"。
  
  容易证明：若\(\large X \sim N(\mu, \sigma^2)\)，则\(\large Y=\dfrac{X-\mu}{\sigma} \sim N(0, 1)\) 。
  
  累积分布函数
• "正态分布" 的pdf(概率密度函数)为“Bell Curve(正态曲线, 钟形曲线)”:
  
  是因为其曲线 呈钟型，两头低，中心高，左右对称。
• 作为一种连续分布，"正态分布" 拥有完备的:
  
  pdf(概率密度函数)、cdf(累积分布函数)、矩生成函数 和 特征函数 等表达形式，
  
  并且有明确的\(\mu\)(期望, 即均值)、\(\sigma^2\)(方差)、偏度 和 峰度 等 数值特征。
• Central Limit Theory(中心极限定理)阐述了, 在一定条件下，多个 独立 同分布的 随机变量 的 平均值 会趋向于"正态分布"，这一现象在 "样本量增大"时"特别显著" 。
• "正态分布" 是 "统计分析和概率论" 的“核心概念”，
  
  在统计学领域具有深远的意义
  
  现实世界，许多 自然和社会现象, 如 考试成绩 和 人体身高 等，都 "近似遵循正态分布"。
  
  其广泛应用于例如"质量控制"、"频数估计" 以及 "制定医学参考标准" 等领域。
• 正态分布的历史:
  • 最初，由法国数学家 Abraham de Moivre(棣莫弗)在1733年引入 , 是其在求“二项分布”的“渐近公式”时发现，但是最初的探索并未深入其在统计学上的应用，尤其是在误差分析方面。
  • 随后，Johann Carl Friedrich Gauss( J. C. F. Gauss, 高斯）提出了关于“正态误差”的理论，并与P-S.Laplace(拉普拉斯) 共同深入研究了“正态分布”的各项特性。

“拟和法”构造出“Bell Curve”

最好是用“基本函数”构造(复合)成的“表达式”，

AUC(曲线下的面积/积分)是 1。

pdf(概率密度曲线方程)

• 曲线是越中心越集中，并且每点的值(概率)都 为正值(大于0)

  • 最常用的"钟形曲线" 而且是"基本函数形式"设为: \(f(x)=x^2\)
  • "总为正值"且"越偏离中心点"的"概率越小", 还是"基本函数形式"设为:\(f(x)=e^{-x}\)

  所以可以先构造(复合)出 \(\large f(x)=e^{-(x^2)}\),

  • 拉普拉斯 首先计算出 \(\large \int{e^{-(x^2)}}d x\) 的值(积分): \(\large \bf{ \sqrt{\pi} }\) ("正态分布" 的规范化常数)。
    
    虽然"现在"能用"求导/积分函数"的"链式法则"轻松求解出\(\large \int{e^{-(x^2)}}d x\) 的值(积分);
    
    但是\(La\ Place\)当时计算出\(\large \bf{ \sqrt{\pi} }\) ("正态分布" 的规范化常数)，
    
    无异于"Newton"计算出"\(\large \bf{G}\)重力加速度常数"是划时代的。

• 概率统计学 的"\(\large \mu(中心值)\)"、"\(\large \sigma(方差)\)"要"能嵌入" 且 "嵌入后的AUC为1(总概率为1)":
  
  首先，嵌入均值: \(f(x)=e^{-(x- \mu )^2}\)，但是其AUC为\(\bf{ \sqrt{\pi} }\),
  
  最终，拉普拉斯在1810年证明并向学院呈现了基本的中心极限定理，强调了正态分布的理论重要性 [18]
  
  然后，调AUC为1:

• 正态分布的pdf(概率密度函数)是一个数学函数，
  
  用于描述 随机变量 在 正态分布 上 取某个特定值 的 概率密度。其公式为：
  
  \(\large f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}\)
  
  注释，

  • μ是均值，
  • σ是标准差。
  • 正态分布的 pdf(概率密度函数)呈现对称的钟形曲线，
    
    在均值处达到最大值，数据在均值附近最集中，越远离均值，数据出现的概率越小。

cdf(累积分布函数:积分面积)

求Bell Curve钟形曲线的AUC(曲线下面积)，

积分？

常规积分？ 黎曼积分？

高斯的 Bell 曲面积分:

将 求解平面(2d)上的 Bell Curve的AUC值\(S\) ，“升维”到求解 “空间(3d)”的 Bell 曲面的VUC(曲面下体积)值\(S^2\)，

即先转换求解“单变量的一重积分”为求解 “两变量的双重积分”。