Loj #3085. 「GXOI / GZOI2019」特技飞行

Loj #3085. 「GXOI / GZOI2019」特技飞行

题目描述

公元 \(9012\) 年，Z 市的航空基地计划举行一场特技飞行表演。表演的场地可以看作一个二维平面直角坐标系，其中横坐标代表着水平位置，纵坐标代表着飞行高度。

在最初的计划中，这 \(n\) 架飞机首先会飞行到起点 \(x = x_{st}\) 处，其中第 \(i\) 架飞机在起点处的高度为 \(y_{i,0}\)。它们的目标是终点 \(x = x_{ed}\) 处，其中第 \(i\) 架飞机在终点处的高度应为 \(y_{i,1}\)。因此，每架飞机可以看作坐标系中的一个点，它的航线是从 \((x_{st},y_{i,0})\) 出发、到 \((x_{ed},y_{i,1})\) 结束的一条线段，如下图所示。

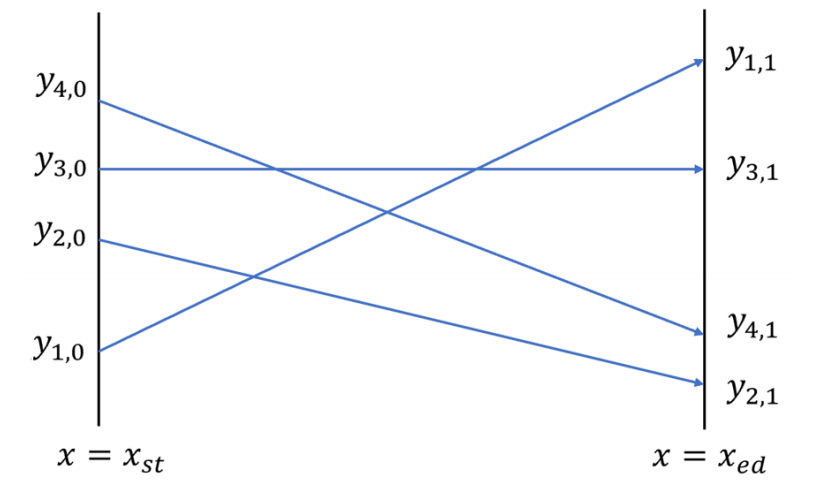
这 \(n\) 架飞机同时出发且始终保持一定的对地速度。因此，对于任意两条交叉的航线（线段），对应的两架飞机必然会同时到达交点处——这就是它们进行特技表演的时刻。它们将会偏转机翼，展现以极近的距离「擦身而过」特技，然后继续保持各自的航线。

航空基地最近还研究了一种新的特技「对向交换」。当两架飞机到达交点处时，之前正在下降的那架立即转为执行抬升动作，之前正在上升的那架则执行一次空翻，两架飞机一上一下、机腹对机腹，同样以极近的距离经过交点，然后互相交换接下来的航线。

我们不必关心特技动作在物理上究竟是如何实现的，飞机仍然看作一个点，在两种特技动作下，航线的变化如下图所示（\(y_{i,1}'\) 表示交换航线后第 \(i\) 架飞机在终点的新高度）。容易发现，「对向交换」会使它们的航线变为折线，并保持它们在纵坐标上的相对顺序；而「擦身而过」会改变它们在纵坐标上的相对顺序。

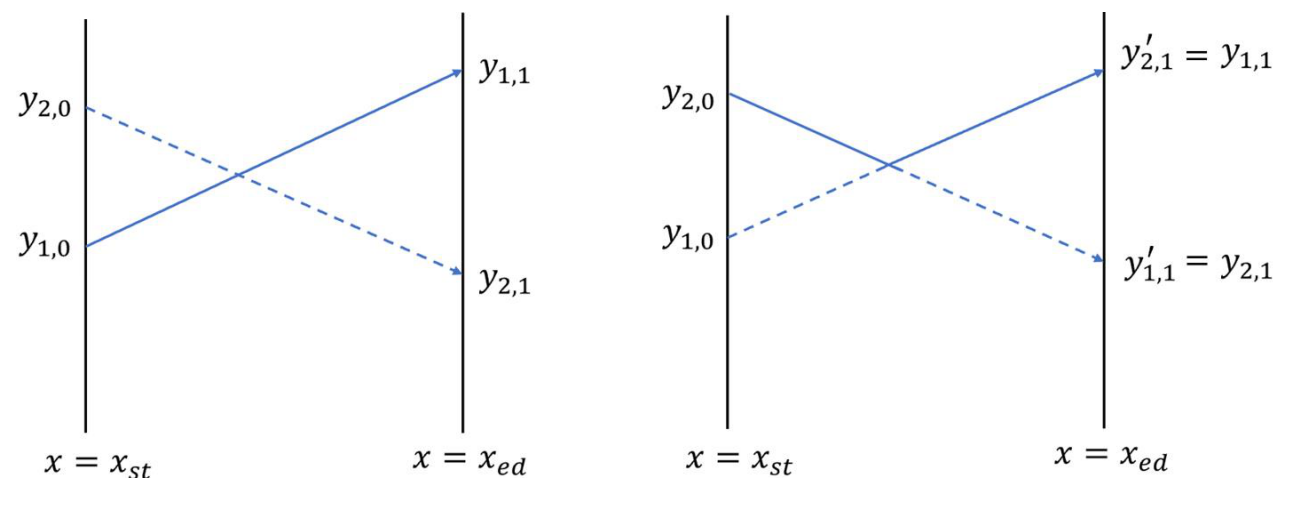
现在，观看表演的嘉宾团提出了一个苛刻的要求——在终点 \(x = x_{ed}\) 处，按照高度排序，\(n\) 架飞机的相对顺序必须与 \(x = x_{st}\) 处的相对顺序一致。嘉宾团还给「对向交换」特技和「擦身而过」特技分别评定了难度系数 \(a\) 和 \(b\)，每次「对向交换」特技可以获得 \(a\) 的分数，每次「擦身而过」特技可以获得 \(b\) 的分数。

除此以外，嘉宾团共有 \(k\) 名成员，第 \(i\) 名成员会乘热气球停留在位置 \((p_i,q_i)\) 处，具有 \(r_i\) 的观测距离，可以观测到区域 \(|x - p_i| + |y - q_i| \le r_i\) 里的所有特技。

若某个交点处的特技被一名或多名嘉宾观测到，则可以获得 \(c\) 的额外加分。

注意：特技无论是否被观测到，均可以获得 \(a\) 或者 \(b\) 的得分。

下图是对本题第一幅图 \(4\) 条航线 \(4\) 个交点的一种满足要求的安排，包括 \(2\) 次「对向交换」、\(2\) 次「擦身而过」，\(3\) 项特技被观测到，得分 \(2a + 2b + 3c\)。为了方便观察，图中展现「对向交换」特技的交点稍稍有些分离。

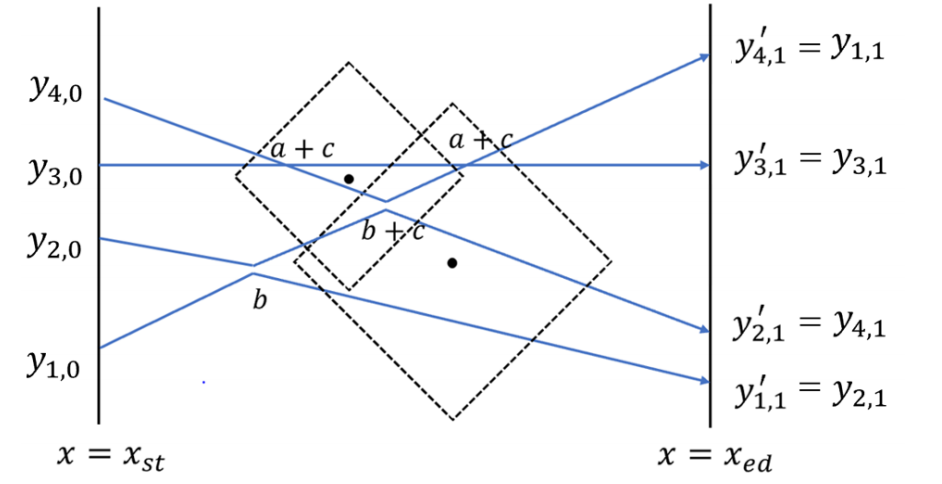
在这次的剧情里，你成为了 Z 市航空基地的规划员，你可以决定在每个交点处是执行「对向交换」还是「擦身而过」。你被要求在保证嘉宾团要求的前提下，计算整个特技表演的可能得到的最低和最高分数。

输入格式

第一行包含六个非负整数 \(n,a,b,c,x_{st},x_{ed}\)，分别表示航线（线段）总数、「对向交换」特技的得分、「擦身而过」特技的得分、观测对表演的额外分、飞行起点的横坐标、飞行终点的横坐标。

第二行包含 \(n\) 个非负整数 \(y_{i,0}\)，其中第 \(i\) 个数表示第 \(i\) 条航线起点的纵坐标，保证按照从低到高的顺序给出，即 \(y_{i,0} < y_{i + 1,0}\)。

第三行包含 \(n\) 个非负整数 \(y_{i,1}\)，其中第 \(i\) 个数表示第 \(i\) 条航线终点的纵坐标。

第四行包含一个非负整数 \(k\)，表示嘉宾的数量。

接下来 \(k\) 行每行三个非负整数 \(p_i,q_i,r_i\)，分别表示第 \(i\) 名嘉宾所在位置的横、纵坐标与观测距离。

输入数据对于所有航线（线段）在直线 \(x = x_{st}\) 和 \(x = x_{ed}\) 之间的交点总数也有一些限制，详见「数据范围与提示」。

输出格式

输出只有一行，包含两个整数，表示整个特技飞行表演的可能得到的最低和最高分数，中间用一个空格隔开。

数据范围与提示

不存在三条或三条以上的线段交于同一点。

所有坐标和 \(r_i\) 均为 \(5 \times 10^7\) 以内的非负整数。

\(y_{i,0} < y_{i + 1,0}\)，\(y_{i,1}\) 各不相同。

\(x_{st} < p_i < x_{ed},1 ≤ a,b,c ≤ 10^3\)。

\(n,k\leq 100,000\)，交点数\(\leq 500,000\)。

\(\\\)

\(c\)对答案的贡献可以旋转坐标系过后扫描线解决。

考虑最大和最小的答案一定是其中一个最大化\(a\)的数量，另外一个最小化\(a\)的数量。\(a\)的最大值就是逆序对（交点）个数（虽然为啥我也不知道）；最小值很显然，将这个序列看做一个置换，那么答案就是\(n-\)循环节个数。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 500005
#define eps 1e-9

using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}

int n;
ll a,b,c,st,ed;
int k;
ll Y0[N],Y1[N];
ll x[N],y[N];
long double d[N];
int rk[N],t[N];
bool cmp(int a,int b) {return Y1[a]<Y1[b];}
struct point {
	long double x,y;
	point() {}
	point(long double _x,long double _y) {x=_x,y=_y;}
	bool operator <(const point &a)const {
		if(fabs(x-a.x)>1e-7) return x<a.x;
		return y<a.y;
	}
}p[N];
int ptot;
void Get_point(int a,int b) {
	long double L=abs(Y0[a]-Y0[b]),R=abs(Y1[a]-Y1[b]);
	long double K=L/(L+R);
	long double x=1.0*st+(ed-st)*K,y=1.0*Y0[a]+(Y1[a]-Y0[a])*K;
	p[++ptot]=point(x-y,x+y);
}

struct Line {
	double x;
	int y1,y2,flag;
	Line() {}
	Line(double _x,int _y1,int _y2,int _flag) {x=_x,y1=_y1,y2=_y2,flag=_flag;}
	bool operator <(const Line &a)const {
		if(fabs(a.x-x)>eps) return x<a.x;
		return flag<a.flag;
	}
}L[N<<2];
int ltot;
int cal1() {
	static bool vis[N];
	int cnt=0;
	for(int i=1;i<=n;i++) {
		if(vis[i]) continue ;
		cnt++;
		for(int j=i;!vis[j];j=rk[j]) vis[j]=1;
	}
	return cnt;
}

ll ans0,ans1;
int low(int i) {return i&(-i);}
int tem[N<<3];
int m;
void add(int v,int f) {for(int i=v;i<=m;i+=low(i)) tem[i]+=f;}
void add(int l,int r,int f) {add(l,f),add(r+1,-f);}
int query(int v) {
	int ans=0;
	for(int i=v;i;i-=low(i)) ans+=tem[i];
	return ans;
}
void discrete() {
	static long double py[N<<3];
	static int ty;
	ty=0;
	for(int i=1;i<=ptot;i++) py[++ty]=p[i].y;
	for(int i=1;i<=k;i++) py[++ty]=y[i]+d[i],py[++ty]=y[i]-d[i];
	sort(py+1,py+1+ty);
	int dy=unique(py+1,py+1+ty)-py-1;
	m=dy;
	for(int i=1;i<=ptot;i++) {
		L[++ltot]=Line(p[i].x,lower_bound(py+1,py+1+dy,p[i].y)-py,0,1);
		if(fabs(py[L[ltot].y1]-p[i].y)>eps) exit(-1);
	}
	for(int i=1;i<=k;i++) {
		int y1=lower_bound(py+1,py+1+dy,y[i]-d[i])-py,y2=lower_bound(py+1,py+1+dy,y[i]+d[i])-py;
		L[++ltot]=Line(x[i]-d[i],y1,y2,0);
		L[++ltot]=Line(x[i]+d[i],y1,y2,3);
	}
}

int cal2() {
	sort(L+1,L+1+ltot);
	int ans=0;
	for(int i=1;i<=ltot;i++) {
		if(L[i].flag==0) {
			add(L[i].y1,L[i].y2,1);
		} else if(L[i].flag==1) {
			if(query(L[i].y1)) ans++;
		} else {
			add(L[i].y1,L[i].y2,-1);
		}
	}
	return ans;
}
int main() {
	n=Get(),a=Get(),b=Get(),c=Get(),st=Get(),ed=Get();
	for(int i=1;i<=n;i++) Y0[i]=Get();
	for(int i=1;i<=n;i++) Y1[i]=Get();
	for(int i=1;i<=n;i++) t[i]=i;
	sort(t+1,t+1+n,cmp);
	for(int i=1;i<=n;i++) rk[t[i]]=i;
	for(int i=1;i<=n;i++) t[i]=0;
	for(int i=1;i<=n;i++) {
		t[i]=i;
		int j=i;
		while(j>1&&rk[t[j-1]]>rk[t[j]]) {
			Get_point(t[j-1],t[j]);
			swap(t[j-1],t[j]);
			j--;
		}
	}
	sort(p+1,p+1+ptot);
	k=Get();
	for(int i=1;i<=k;i++) {
		x[i]=Get(),y[i]=Get(),d[i]=Get();
		ll X=x[i]-y[i],Y=x[i]+y[i];
		x[i]=X,y[i]=Y;
	}
	ll cnt=n-cal1();
	ans0=cnt*a+(ptot-cnt)*b;
	ans1=ptot*a;
	ll sp=0;
	for(int i=1;i<=ptot;i++) {
		long double X=p[i].x-p[i].y,Y=p[i].x+p[i].y;
		for(int j=1;j<=k;j++) {
			if(fabs(p[i].x-1.0*x[j])<=d[j]&&fabs(p[i].y-1.0*y[j])<=d[j]) {
				sp++;
				break;
			}
		}
	}
	discrete();
	int watch=cal2();
	ans0+=watch*c,ans1+=watch*c;
	if(ans0>ans1) swap(ans0,ans1);
	cout<<ans0<<" "<<ans1;
	return 0;
}