[GXOI/GZOI2019]与或和（位运算，单调栈）

题目链接懒得放了。

题目大意懒得写了。

省选原题哪有找不到的……

---

说实话，其实这题是个大水题，被我十秒钟内口胡出来了。

首先位运算除了拆位还能干啥？以下以与为例，或是差不多的。

我们考虑有多少个子矩阵会对这一位答案产生贡献，其实就是全 $1$ 的子矩阵。

问题转化为计算全 $1$ 子矩阵的个数。

这是一个简单题。考虑枚举右下角，发现包括这个右下角的子矩阵肯定长这样：（画的比较丑，意会就好了）

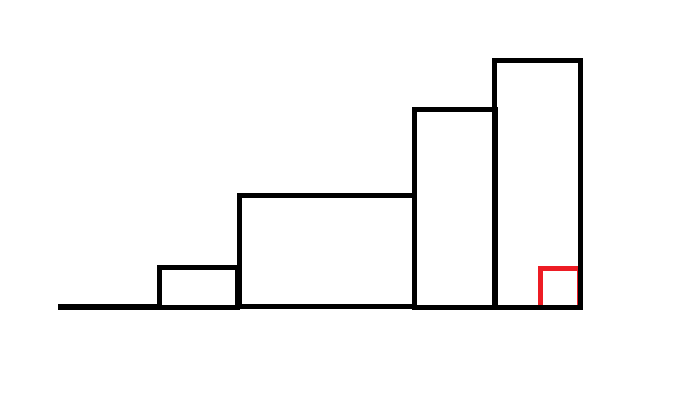
也就是高度单调递增。

高度可以做到 $O(1)$ 转移（从 $h[i-1][j]$）转移。

至于递增的高度，直接一个单调栈。（设为 $s$）

那么这个点为右下角的矩阵个数为 $(s_1-s_0)h[i][s_1]+(s_2-s_1)h[i][s_2]+\cdots+(s_{top}-s_{top-1})h[i][s_{top}]$。这个也可以入出栈时随便更新一下。

时间复杂度 $O(n^2\log a_i)$。

（然而一开始式子推错了，调了好久，回来再看看发现自己就是个sb……）

#include<bits/stdc++.h>
using namespace std;
const int maxn=,mod=;
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline int read(){
    char ch=getchar();int x=,f=;
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int n,a[maxn][maxn],b[maxn][maxn],ans1,ans2,h[maxn],stk[maxn],tp,sum;
int calc1(){
    int ans=;
    MEM(h,);
    FOR(i,,n){
        MEM(stk,);tp=sum=;
        FOR(j,,n) h[j]=b[i][j]?h[j]+:;
        FOR(j,,n){
            while(tp && h[j]<h[stk[tp]]){
                sum=(sum-1ll*h[stk[tp]]*(stk[tp]-stk[tp-])%mod+mod)%mod;
                tp--;
            }
            stk[++tp]=j;
            sum=(sum+1ll*h[stk[tp]]*(stk[tp]-stk[tp-]))%mod;
            ans=(ans+sum)%mod;
        }
    }
    return ans;
}
int calc2(){
    int ans=;
    MEM(h,);
    FOR(i,,n){
        MEM(stk,);tp=sum=;
        FOR(j,,n) h[j]=b[i][j]?:h[j]+;
        FOR(j,,n){
            while(tp && h[j]<h[stk[tp]]){
                sum=(sum-1ll*h[stk[tp]]*(stk[tp]-stk[tp-])%mod+mod)%mod;
                tp--;
            }
            stk[++tp]=j;
            sum=(sum+1ll*h[stk[tp]]*(stk[tp]-stk[tp-]))%mod;
            ans=(ans+sum)%mod;
        }
    }
    int tot=1ll*n*(n+)*n*(n+)/%mod;
    return (tot-ans+mod)%mod;
}
int main(){
    n=read();
    FOR(i,,n) FOR(j,,n) a[i][j]=read();
    FOR(_,,){
        FOR(i,,n) FOR(j,,n) b[i][j]=(a[i][j]>>_)&;
        ans1=(ans1+1ll*calc1()*(<<_))%mod;
        ans2=(ans2+1ll*calc2()*(<<_))%mod;
    }
    printf("%d %d\n",ans1,ans2);
}