由题意知，爆破可行。

简单说一下抓包过程，第一个抓到的POST包直接放掉，右键扫描站点，扫出来第二个POST包，第二个POST包cookie，验证码，密码均为空，于是我开始尝试去利用，

经过几次repater测试过后，发现，返回包只返回密码错误，而不是验证码错误，于是拿去直接爆破。

抓包发现，验证码没有用到，只是一个摆设

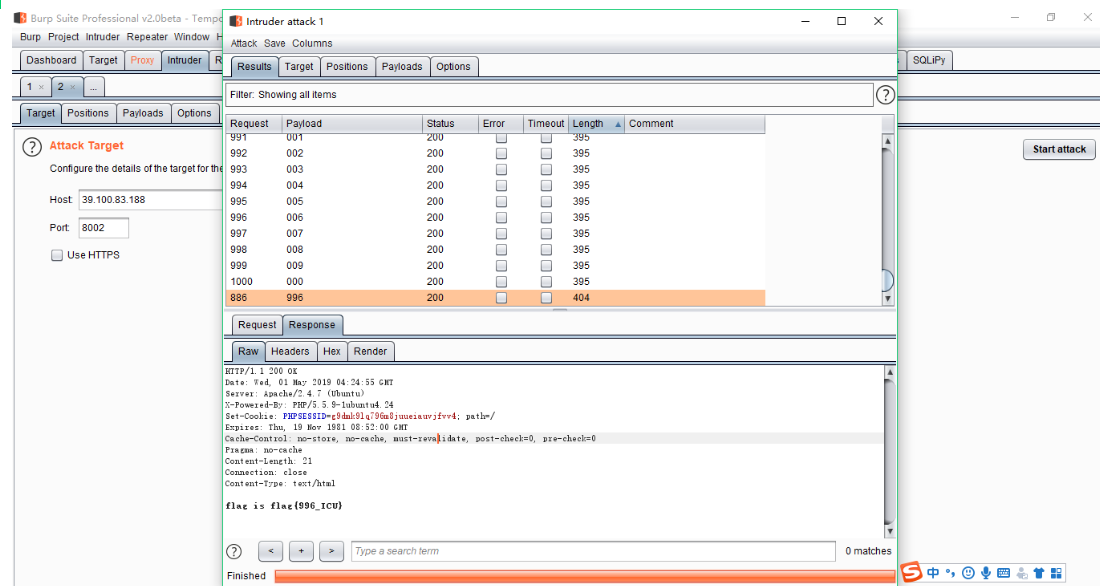
flag is flag{996_ICU}

ISCC之web1的更多相关文章

  1. ISCC 2018线上赛 writeup

    今天有机会去ISCC2018参加了比赛,个人的感受是比赛题目整体难度不高,就是脑洞特别大,flag形式不明确,拿到flag后也要猜测flag格式,贼坑 废话不多说,以下是本人的解题思路 MISC 0x ...

  2. Web1.0、Web2.0、Web3.0的主要区别

    Web1.0:以静态.单向阅读为主,网站内信息可以直接和其他网站信息进行交互,能通过第三方信息平台同时对多家网站信息进行整合使用. Web2.0:以分享为特征的实时网络,用户在互联网上拥有自己的数据, ...

  3. 从ASP.NET的web1子界面刷新打开web1的web0父界面

    单击web0界面的按钮bt1触发一下代码: protected void btnSave_Click(object sender, EventArgs e) { string parentJs = @ ...

  4. ISCC 2018 Writeup

    题解部分:Misc(除misc500).Web(除Only Admin.Only admin can see flag.有种你来绕.试试看).Reverse.Pwn.Mobile Misc( Auth ...

  5. ISCC 2018(数字密文）

    做过iscc 2018之后有了很多的感触,也有更多的了解自己的不足之处,整理了一下web的wp, 为了保证各位小伙伴的阅读质量,我将会把wp以每一道题一个博文的形式写出来,希望能够帮助到你们 其中的步 ...

  6. ISCC 2018 (Please give me username and password)

    做过iscc 2018之后有了很多的感触,也有更多的了解自己的不足之处,整理了一下web的wp, 为了保证各位小伙伴的阅读质量,我将会把wp以每一道题一个博文的形式写出来,希望能够帮助到你们 其中的步 ...

  7. 【CTF WEB】ISCC 2016 web 2题记录

      偶然看到的比赛,我等渣渣跟风做两题,剩下的题目工作太忙没有时间继续做. 第1题 sql注入: 题目知识 考察sql注入知识,题目地址:http://101.200.145.44/web1//ind ...

  8. ISCC的 Misc——WP

    比赛已经结束了,自己做出来的题也不是很多,跟大家分享一下 Misc 第一题:What is that? 下载链接; 打开 解压 是一个图片 因为分值很少所以题和简单 观察图片是一个向下指的手 说明fl ...

  9. ISCC 2018——write up

    WEB Web1-比较数字大小 直接修改input 标签里的maxlength 为999突破长度限制,使得能输入大于999 的数,然后随便输一个数字就行了 或者post修改值 Web2-Web01 s ...

随机推荐

  1. Kafka生产者性能优化之吞吐量VS延迟

    When we are talking about performance of Kafka Producer, we are really talking about two different t ...

  2. zookeeper学习整理

    概述 zookeeper是一个高可用的分布式数据管理与协调框架,基于ZAB算法实现,主要解决分布式一致性问题. https://www.cnblogs.com/felixzh/p/5869212.ht ...

  3. LInux学习之路

    linux 简单操作命令 cd 进入目录 ls 查看 ll详细查看 man ls -- help touch mkdir find 正则表达式 ? [] [a-z][0-9] {字符串,} {a..z ...

  4. 使用pyinstaller将python打包成exe文件

    步骤: 1)win+R 输入cmd打开dos窗口   2)先安装pyinstaller: pip install pyinstaller 3)然后使用cd命令进入项目文件的路径下:   4)再使用命令 ...

  5. layui 监听switch事件

    <input type="checkbox" lay-filter="common_change_status" name="switch&qu ...

  6. LeetCode 290. 单词规律(Word Pattern) 41

    290. 单词规律 290. Word Pattern 题目描述 给定一种规律 pattern 和一个字符串 str,判断 str 是否遵循相同的规律. 这里的 遵循 指完全匹配,例如,pattern ...

  7. linux 环境搭建

    1.安装jdk 上传tar包,解压缩 vim /etc/profile JAVA_HOME=/usr/local/jdk1.8.0_152CLASSPATH=$JAVA_HOME/lib/PATH=$ ...

  8. [转帖]GNU， Free Software and Open Source 自由软件与开源软件

    GNU, Free Software and Open Source 自由软件与开源软件 https://blog.csdn.net/icycolawater/article/details/7792 ...

  9. Linux学习-防火墙-Selinux-配置本地YUM源

    关闭防火墙并设置开机不启动 systemctl status firewalld.service #查看firewalld状态systemctl stop firewalld #关闭systemctl ...

  10. C语言函数库帮助文档

    C语言函数库帮助文档 安装 1.C语言库函数基本的帮助文档 sudo apt-get install manpages sudo apt-get install manpages-de sudo ap ...