[清华集训2017]小 Y 和地铁（神奇思路，搜索，剪枝，树状数组）

世界上最不缺的就是好题。

首先考虑暴搜。（还有什么题是从这东西推到正解的……）

首先单独一个换乘站明显没用，只用考虑一对对的换乘站。

那么有八种情况：（从题解偷图）

       

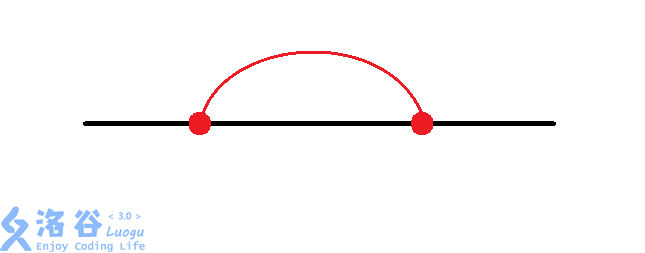
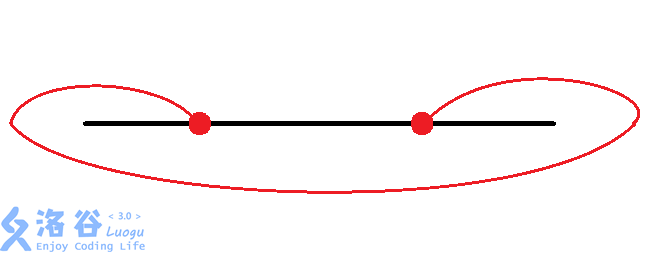
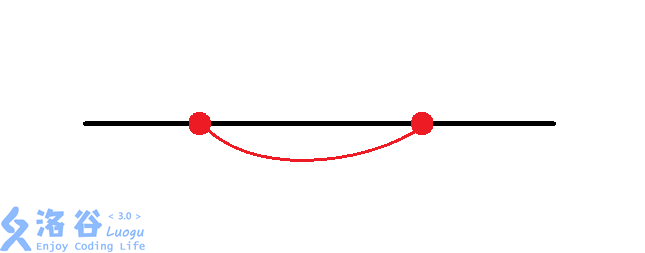
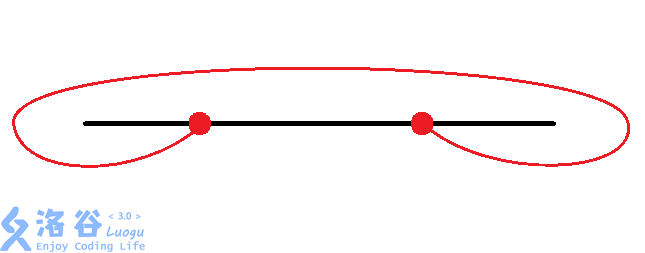
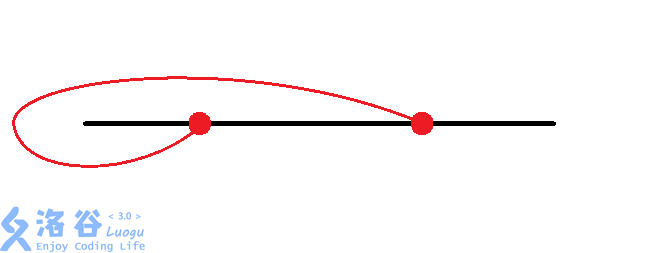
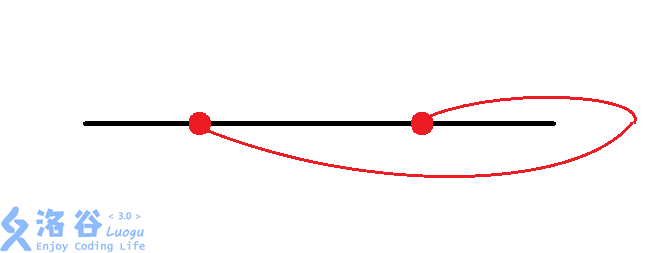
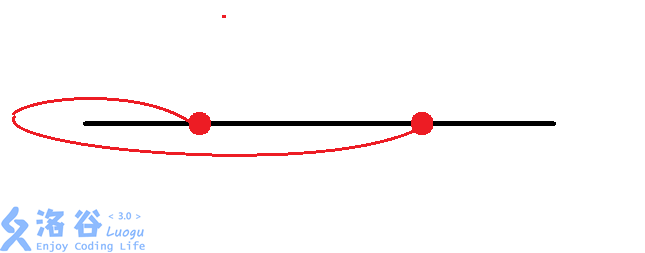
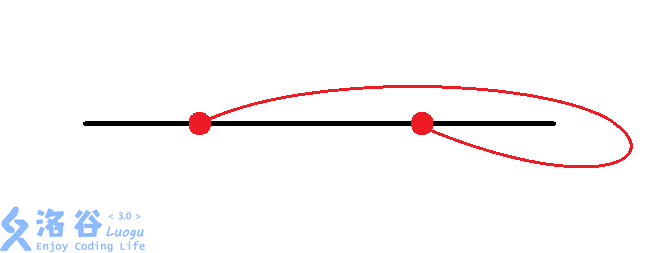
然后大力枚举每个换乘站的情况。同时判断交点。$O(n\times 8^{\frac{n}{2}})$。

然后考虑这种情况：

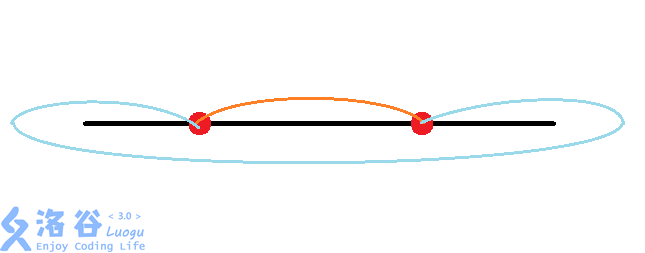
发现对于任意一条地铁线，要么与这两个都有交点，要么可以与这两个都没有交点。（其实会有与一个有两个交点，与另一个没有交点的情况。这时也可以把这条线换个方向，答案不会更差。思考思考为什么）

那么合法状态只剩四种：

   

再考虑这两个线路：

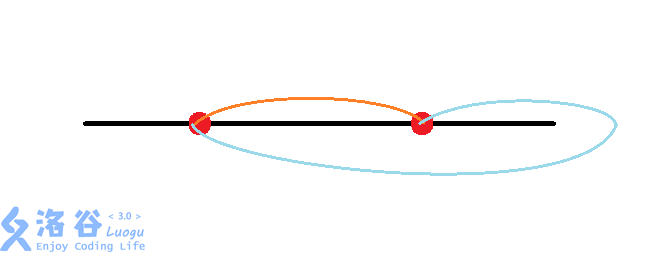
发现，虽然对于左端点在第一个红点右边的地铁线，这两种没有区别，但是对于左端点在第一个红点左边的地铁线，它们可能有区别。
不过由于我们搜索是按左端点从小到大搜的，所以可以贪心取目前这两条线最优的一条，不会影响后面的值。

最后每次合法状态只剩两个。$O(n\times 2^{\frac{n}{2}})$。

此时合法状态不可能再减少了。考虑加速求交点个数。

发现对于左端点小于当前地铁线的左端点的地铁线，与这个地铁线有交点当且仅当右端点在一个区间（具体看代码）内。

那么可以用树状数组优化。每次给右端点打个标记，然后就变成了求区间和。

$O(2^{\frac{n}{2}}\log n)$。

p.s：要调用很多次树状数组，常数也不小，我就挂了，挂成 80 分。

然而加上个普及组剪枝就过了。$sum>ans$ 时 $return$。

（普及组搜索剪枝不会了……智商越来越低了）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=;
#define FOR(i,a,b) for(int i=(a);i<=(b);i++)
#define ROF(i,a,b) for(int i=(a);i>=(b);i--)
#define MEM(x,v) memset(x,v,sizeof(x))
inline int read(){
    int x=,f=;char ch=getchar();
    while(ch<'' || ch>'') f|=ch=='-',ch=getchar();
    while(ch>='' && ch<='') x=x*+ch-'',ch=getchar();
    return f?-x:x;
}
int t,n,m,tp[maxn],l[maxn],r[maxn],ans,sum,b[][maxn];
inline void update(int id,int p,int v){
    while(p<=n){
        b[id][p]+=v;
        p+=p&-p;
    }
}
inline int query(int id,int p){
    int s=;
    while(p){
        s+=b[id][p];
        p-=p&-p;
    }
    return s;
}
inline int query(int id,int l,int r){return query(id,r)-query(id,l-);}
void dfs(int dep){
    if(sum>ans) return;
    if(dep>m) return void(ans=sum);
    int t1=query(,l[dep],r[dep]),t2=query(,r[dep],n),t3=query(,l[dep],r[dep]),t4=query(,r[dep],n);
    update(,r[dep],);
    sum+=min(t1,t2+t3+t4);
    dfs(dep+);
    sum-=min(t1,t2+t3+t4);
    update(,r[dep],-);
    update(,r[dep],);
    sum+=min(t3,t1+t2+t4);
    dfs(dep+);
    sum-=min(t3,t1+t2+t4);
    update(,r[dep],-);
}
int main(){
    t=read();
    while(t--){
        m=;ans=1e9;
        n=read();
        FOR(i,,n) tp[i]=read();
        FOR(i,,n) FOR(j,i+,n) if(tp[i]==tp[j]) l[++m]=i,r[m]=j;
        dfs();
        printf("%d\n",ans);
    }
}