PKUSC2019 改题记录

我真的是个sb。。。

警告：不一定是对的。。。

D1T1

有一个国家由\(n\)个村庄组成，每个村庄有一个人。对每个\(i\in[1,n-1]，\)第\(i\)个村庄到第\(i+1\)个村庄有一条边。村民的移动方式是选择两个相邻的村庄，交换这两个村庄里的人。每年人们都想出去旅游，每年结束时第\(i\)个村庄里的人想去第\(p_i\)个村庄，保证\(p\)是一个排列。

政府会在一些路上收取过路费。在每年的开始，会有一条路上加入哨卡。在一次移动中，如果移动涉及到的路上有哨卡，或者移动涉及到的两个人在这一年经过过哨卡，就要支付1过路费。村民们想最小化每年需要支付的过路费之和。当一年结束，村民都到达目标点之后，会瞬间回到原来的村庄。

\(n\leq 10^6\)。

答案是经过了哨卡的逆序对之和。

那么从后往前线段树合并一下就行了。

D1T2

有\(2n\)个同学在\(n\)个球桌上打比赛，一共有\(m+1\)轮。第一轮比赛方案已经确定好，在一轮时每一桌双方会进行一场比赛。同学的编号代表他的实力，一场比赛时，编号小的同学有\(\frac 13\)的概率获胜。第\(i(i>1)\)轮时：

第\(1\)桌由上一轮第\(1\)桌和第\(2\)桌的败者组成；
第\(j(j\in[2,n-1])\)桌由上一轮第\(j-1\)桌的胜者和第\(j+1\)桌的败者组成；
第\(n\)桌由上一轮第\(n-1\)桌和第\(n\)桌的胜者组成。

对于所有的\(i,j\)求第\(m+1\)轮\(i\)同学在第\(j\)个桌子比赛的概率。

\(n\leq 9,m\leq 20\)。

当然可以直接状压，但是会T。

对每个数\(i\)将编号\(\leq i\)设为\(0\)，\(>i\)设为\(1\)，这样状压就行了，总的状态数是\(3^n\)的。

一次转移的复杂度是\(\sum_{i=0}^{3^n-1}2^{\sum_{j=0}^{n-1}[i[j]=0]}\)的，\(i\)是个三进制数，\(i[j]\)是\(i\)在第\(j\)位的值。

D1T3

有\(n\)个数，第\(i\)个数是\(a_i\)。

有\(q\)个询问，第\(i\)个询问形如\(x,y\)，表示询问是否存在一个\(k\)使得序列所有数都异或\(k\)后，第\(x\)个数排名为\(y\)。

\(n\leq 50000,q\leq 1000000,a_i<2^{60}\)。

对每个询问，从踹树上走到\(a_x\)，走一步时，如果要从\(p\)走到\(ch_{p,0}\)，那么可以选择将排名增加\(sum_{ch_{p,1}}\)。就是一个bitset优化背包。这样是\(O(nq\log a/w)\)的。

显然相同的\(x\)可以一起处理，那么复杂度降为\(O(n^2\log a/w)\)。

在踹树上搜索边搜边维护bitset，如果这个点只有一个儿子就不用转移这个背包。多余一个儿子的点数显然\(O(n)\)，复杂度成功优化到\(O(n^2/w)\)。

D2T1

有一棵\(n\)个点的树，要给这棵树染色，有\(m\)种颜色。相邻两个点颜色不能相同，还有\(k\)个限制，每个限制形如\(x,y\)，表示第\(x\)个点不能染颜色\(y\)。求染色方案数。

\(n\leq 200000,m\leq 10^9,k\leq 100000\)。

显然的dp就不说了。

显然一个子树里，除了在这个子树中有被限制过的颜色外，dp值都相同。

那么只用记有限制过的颜色的dp值和其他的dp值，用线段树记，转移在线段树合并时进行。我现场的操作需要用到区间乘矩阵~~所以卡常了1h~~想不到常数更优秀的办法了。

D2T2

有一棵\(n\)个点的树，你要构造一个\(m\)维空间以及\(n\)个点\((x_{i,1},x_{i,2},\cdots,x_{i,m})\)，使得对任意的\(i,j\)，满足\(i,j\)在树上的距离等于在空间里的曼哈顿距离。

如果有多种方案，你需要在\(m\)最小的前提下输出任意一个。

\(n\leq 100\)。

有一种想法，就是把树分成若干条边不交的链，然后每条链开一维，然后这一维的方法就是这条链按顺序标号，其他点这一维的值是离得最近的这条链上的点的标号。

发现可以优化，假如有一棵树是这样的：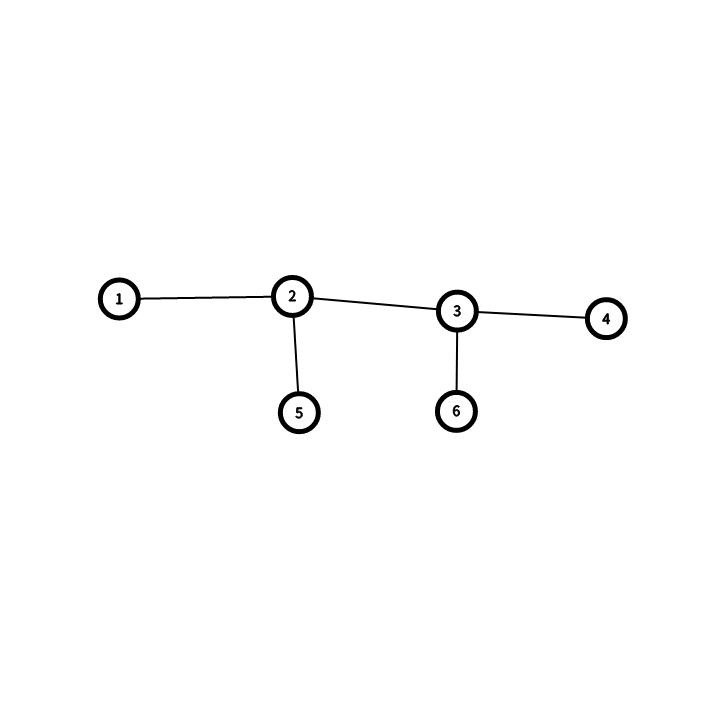

然后你分了链1-2-3-4，链2-5，链3-6。这个2-5和3-6链是可以拼起来的。拼成新的一维，这一维可以看作是一条链，但是和其他链重复的边的两边标号相等。比如2-3边，这一维的标号就相等。这条新的链可看做5-(2,3)-6。

这样的可行方案是：(1,2),(2,2),(3,2),(4,2),(2,1),(3,3)。

两条链拼成新的链很蠢，实际上就是选若干条链，可重复地覆盖这棵树，然后每条链开一维。

那么是这个题。https://loj.ac/problem/2371

注意：方案对的但我不保证m一定最小。但是有考场切了的说我这个和他一样，那就是最小的吧。。。

UPD：有一个下界是叶子节点除以2向上取整，好像可以达到，那就是最小的吧。。

D2T3

定义弦线图表示线图是弦图的图。

有一棵树，你要加入任意条无向边，求新图是弦线图的方案数。

\(n\leq 200000\)。

首先是仙仙图的充要条件是没有\(\geq 4\)个点的环。

那么新加的边只能连距离为2的点，而且不能相交（脑补一下）新加的这条边会覆盖这两个点之间的树边，每条树边只能被覆盖一次。

这就是一个沙雕dp了。设\(f[i][0/1]\)表示\(i\)这个点子树中的方案数，\(i\)到父亲的边没选/选了。

那么只需要看到儿子的边还没选的那些，而且方案数之和这个有关。

设\(g[i][0/1]\)表示一个点有\(i\)个儿子的边可以选的方案数，这个点到父亲的边没选/选了。

那么\(g[i][0]=g[i-1][0]+g[i-2][0](i-1)\)，\(g[i][1]=g[i-1][1]+g[i-2][1]\cdot(i-1)+g[i-1][0]\)。

有\(i\)个儿子可以选的所有方案的\(f\)之和可以分治ntt。

就做完了。