机器学习 降维算法: isomap & MDS

　　最近在看论文的时候看到论文中使用isomap算法把3D的人脸project到一个2D的image上。提到降维，我的第一反应就是PCA,然而PCA是典型的线性降维，无法较好的对非线性结构降维。ISOMAP是‘流形学习’中的一个经典算法，流形学习贡献了很多降维算法，其中一些与很多机器学习算法也有结合，先粗糙的介绍一下’流形学习‘。

　　流形学习

　　流形学习应该算是个大课题了，它的基本思想就是在高维空间中发现低维结构。比如这个图：

　　

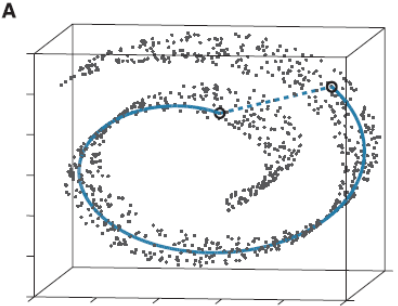
　　这些点都处于一个三维空间里，但我们人一看就知道它像一块卷起来的布，图中圈出来的两个点更合理的距离是A中蓝色实线标注的距离，而不是两个点之间的欧式距离（A中蓝色虚线）。

　　此时如果你要用PCA降维的话，它根本无法发现这样卷曲的结构（因为PCA是典型的线性降维，而图示的结构显然是非线性的），最后的降维结果就会一团乱麻，没法很好的反映点之间的关系。而流形学习在这样的场景就会有很好的效果。

　　经典MDS（Multidimensional Scaling）
　　如上文所述，MDS接收的输入是一个距离矩阵DD,我们把一些点画在坐标系里：

　　

　　如果只告诉一个人这些点之间的距离（假设是欧氏距离），他会丢失那些信息呢？
　　a.我们对点做平移，点之间的距离是不变的。
　　b.我们对点做旋转、翻转，点之间的距离是不变的。

　　所以想要从D还原到原始数据X是不可能的，因为只给了距离信息之后本身就丢掉了很多东西，不过不必担心，即使这样我们也可以对数据进行降维(why？点这里)。

　　ISOMAP(等距特征映射)

　　其实线性流形方法无法在非线性流形上解决的问题，无非是需要解决两个问题：

　　1、如何测量流形上的几何距离？

　　2、如何将高维的2016维欧式空间映射到三维的低维空间？

　　首先，针对问题1，将MDS算法中的欧式距离换成“测地距离”，先抛一个“测地线的维基定义”。预热以后，我们来看经典的瑞士卷（图A），注意以下图A、B、C均来源于原文论文Fig3截图：

　　

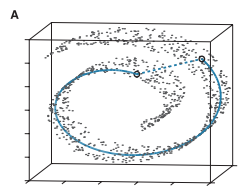
　　现在要我们把自己想象成是瑞士卷上的蚂蚁（对人类来说瑞士卷是三维的，对蚂蚁来说是二维的），上图A中的两个黑色圈圈为两只恩爱无比的蚂蚁，如何让这两只蚂蚁在最短的时间内见面呢？要走最短路径测地线蓝色线才是正道（直线最短？直接沿着虚线强行阔过去？你不想活了么？）因此，抛弃欧式距离，引来测地距离～

　　邻近点：直接计算邻近点之间的欧式空间距离

　　远距离的点：计算邻近点之间的最短距离连接成的序列，如下图所示（来源于博客），要计算空间中远距离的亮点1与9，计算1到9的最短路径1、2、3...9，沿着路径依次类推直到到达目的地9（根据流形中的全局非线性和局部线性属性）：

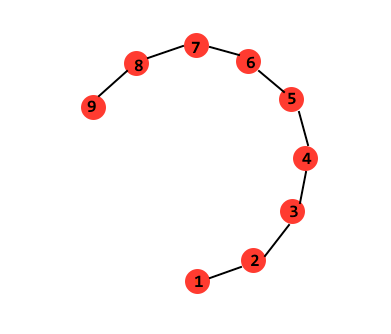
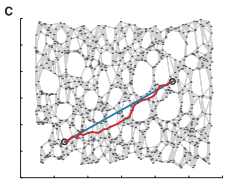
　　最后形成如下图所示的瑞士卷上的逼近测地线，如下图B中的红色线条所示：

　　

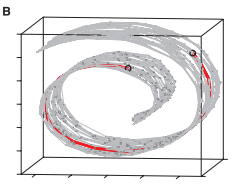
　　实现方法：引入图论框架，将数据作为图中的点，点与其邻近点之间使用边来连接，逼近的测地线使用最短路径代替。

　　 Isomap算法流程如下：

　　 步骤1：构建邻接图G（复杂度：O（DN²））

　　 基于输入空间X中流形G上的的邻近点对i,j之间的欧式距离d_x (i,j)，选取每个样本点距离最近的K个点（K-Isomap）或在样本点选定半径为常数ε的圆内所有点为该样本点的近邻点，将这些邻近点用边连接，将流形G构建为一个反映邻近关系的带权流通图G；

　　 步骤2：计算所有点对之间的最短路径（复杂度：O（DN²））

　　 通过计算邻接图G上任意两点之间的最短路径逼近流形上的测地距离矩阵D_G={d_G(i,j)}，最短路径的实现以Floyd或者Dijkstra算法为主。

　　 步骤3：构建k维坐标向量（复杂度：O（dN²））

　　 根据图距离矩阵D_G={d_G(i,j)}使用经典Mds算法在d维空间Y中构造数据的嵌入坐标表示（如下图C所示），选择低维空间Y的任意两个嵌入坐标向量y_i与y_j使得代价函数最小：

　　

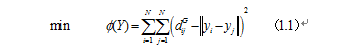
　　其中等式1.1的全局最优解可以通过将坐标向量y_i设置为距离矩阵D_G前d个特征值对应的特征向量来得到。

　

(还是偷懒了，没有去看看具体的例子，要用的时候再说把23333)

Reference:

[1] https://blog.csdn.net/dark_scope/article/details/53229427

[2] https://www.cnblogs.com/wing1995/p/5479036.html