Folx专业版智能速控功能详解

限速功能指的是，用户可以通过限制最大上传、下载速度来控制任务下载的带宽使用，减少因下载导致其他应用程序出现网络延迟的情况。Folx不仅为用户提供简单的任务限速功能，而且还提供更加智能的速控功能，供用户更加灵活地进行限速设置，既能保证下载任务的快速完成，又能确保其他应用程序的正常使用。

图1：软件界面

一、智能速控功能

首先，小编要介绍的是Folx的智能限速功能。

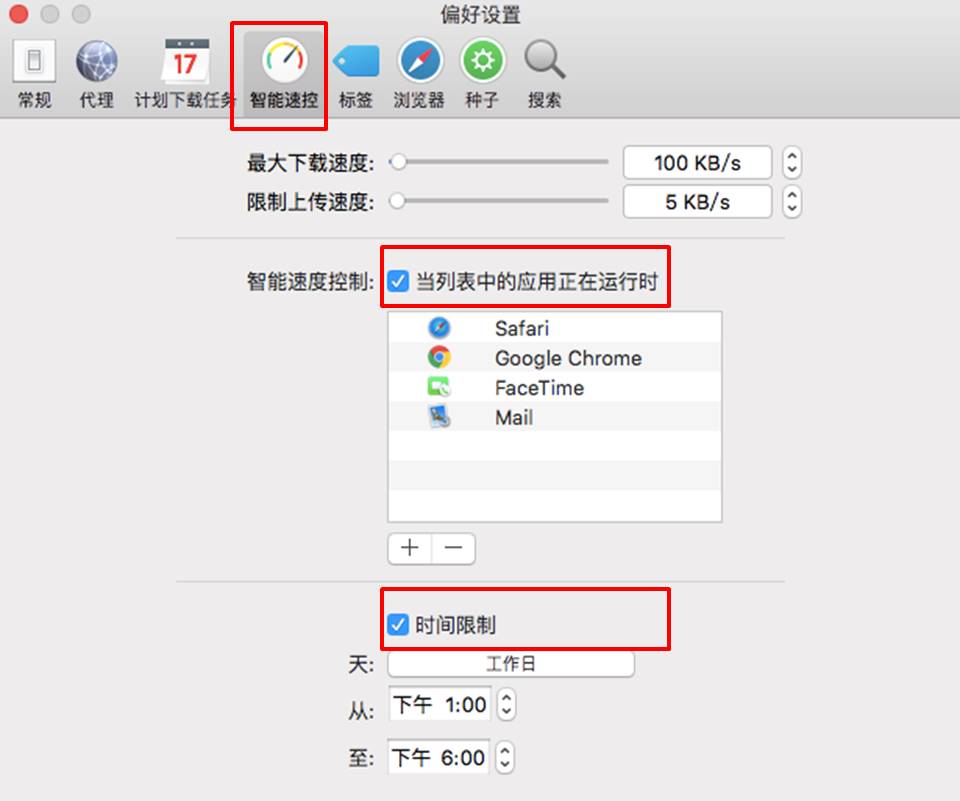
如图2所示，打开软件顶部的Folx菜单，并选择其中的偏好设置选项。

图2：偏好设置

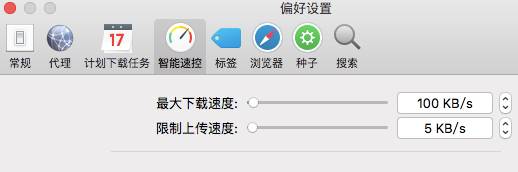
然后，在偏好设置的智能速控选项卡中，用户就能利用程序限制选项、时间限制选项来进行智能限速设置。

比如，如图3所示，当系统在工作日的下午1:00-6:00之间运行FaceTime程序时，Folx就会自动执行智能速度控制，将最大下载速度限制为100KB/s、限制上传速度为5KB/s，确保FaceTime能正常使用带宽资源，防止出现网络延迟的情况。

图3：智能速控功能

二、整体限速

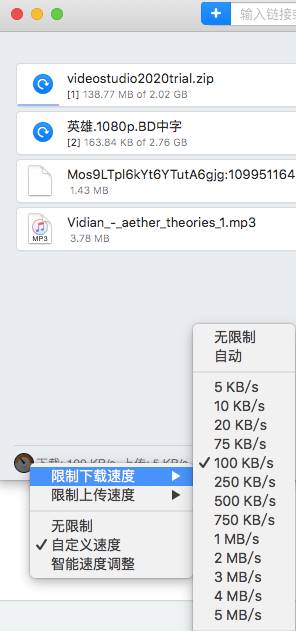
用户如果只是希望进行简单的整体限速，以限制整个Folx的带宽使用，可以直接单击软件左下角的限速按钮，在其选项中选择限制下载速度或限制上传速度，然后再选择具体的限速数值即可。

当然，用户也可以选择“自动”，让Folx自行进行速度限制设置。

图4：整体限速

三、单个任务限速

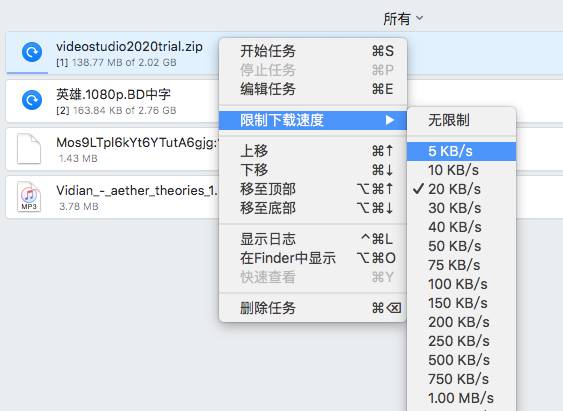
最后，用户如果希望对单个下载任务进行限速，可以直接右击下载任务，然后在其右键快捷菜单中选择“限制下载速度”，就可以指定具体的限速数值。该方法很适合用于一些下载速度较快的资源或紧急性不高的资源，以减少过多的带宽占用。

图5：单个任务限速

通过以上的叙述，相信大家已经对Folx专业版的速度限制功能有了更多的了解。如果您也想体验专业版的限速功能，可以前往Folx中文网站进行软件的激活。另外，Folx专业版还有很多实用的功能值得您进一步探索。