Numerical Sequence（hard version)，两次二分

题目：

　　　　

　　　　

　　　　

　　　　

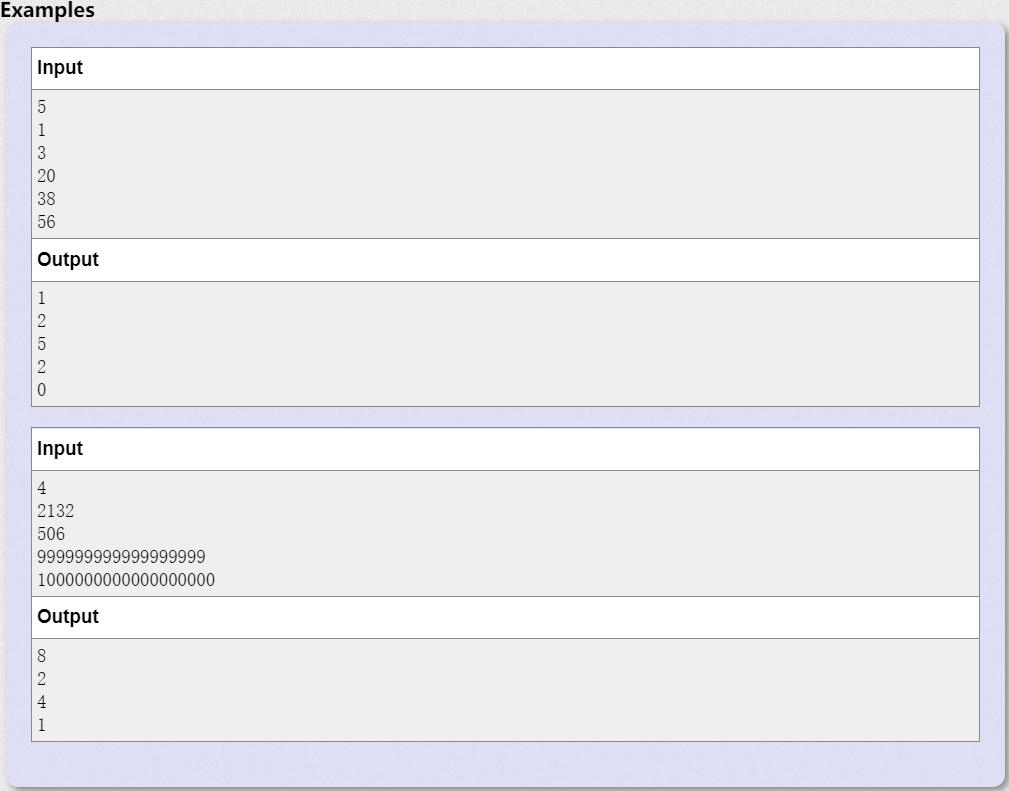
题意：

　　已知一个序列：

　　　　112123123412345123456123456712345678123456789123456789101234567891011。。。

　　求这个序列第k个数是多少。

分析：

　　首先，我们先来看这样一个问题，让求123456789101112131415。。。一直到n的长度是多少，我们会怎么求呢？显然，我们会分开求：1-9一组，10-99一组，100-999一组。。。当然组数不会很多，然后组内其实就是一些位数相等的数的位数的和，那么当然用乘法解决，数清项数就好了，显然第i组的项数（即有几个位数为此组位数的数）是P（i）-P（i-1）（P（a）表示10的a次方），然后每一个数的长度就是i，当然注意一下最后一组的特殊处理。

　　求得这个之后有什么用呢？我们可以用它来求什么，我们这样想：其实原序列就是由我们刚求出来的序列组成的，那么是不是我们可以直接根据上面的求法把1到s相加求得以1-s结尾的序列的长度，显然，并不能，这个数字出奇的大，是多少呢？一会儿会用到，一会儿再说，我们先考虑怎么简化运算，显然，可以和上面的处理一样，我们分开处理，1-9，10-99。。。这些怎么处理呢？一会发现，这些其实是一些等差数列，如：1-9是公差为1的等差数列，10-99是公差为二的等差数列，而首项就是我们之前可以求的1-P（i-1）的和这样的话就可以直接带公式求等差数列和了，还有就是边界，处理了最大的就好了。

　　现在我们可以求着个序列到哪里是多大了，但是给我们的是长度啊，那就要二分了，二分之后我们便确定了这个序列是在1234。。。到几的一个序列里，是这个的第几位呢？减取前面的就能求出来了，但是知到了是第几位并不能很快的求出是多少，但是没有关系，再次二分，可以确定最后他比1-x多多少，然后就找到x+1的第多出来的哪一位（从高向低数）就好了，这个的复杂度还是比较有保证的：最多也超不过20*20*40*500（有些数字稍微记大了一些），然后就是二分的左右边界，这个只能去试了，算一下多少超了10的18次方还没爆long long就好了。

　　好的那么我们再想这样一个问题（别急着看代码）：现在我们给你这样的一堆数：

　　1

　　112

　　112123

　　1121231234

　　112123123412345

　　112123123412345123456

　　。。。

求第k个数字，这样其实还是类似的，只不过是再把原序列重复的写了几遍，这样大家顺着刚才的思路也可以想到了吧，我们可以先确定在哪一行，再去找数，这个式子怎么算呢？（差值为等差数列的数列求和）高斯的某个定理好像可以算这个，不过，如果不想推公式，还有一种方法：其实这时候我们的最多大已经比较小了我们只需要记录数组然后二分就可以了。

　　1-x：a[i]=a[i-1]+ws（i）             (ws表示i的位数)

　　原题给的序列：b[i]=b[i-1]+a[i];

　　新定义的这个序列：c[i]=c[i-1]+b[i]

　　处理一下多二分几次就好了。

　　ws的计算是log的，我们不太喜欢，没关系，其实你会发现，大部分情况w是不变的即w[i]=w[i-1]，只有i是10的整数次方时才变，那么就好办了，只有记录上一个10的整数次方是多少，然后如果它*10等于这个数，那么就w[i]=w[i-1]+1，当然，w数组可以不开，拿个变量记录一下就好了

　　那么我们继续想；

　　数组

　　d[i]=d[i-1]+c[i]

　　可以构造出含意吗，当然可以，表示一群那个类似矩阵的东西的和（能想像出来吧），当然，这样其实我们没必要要些换行，只要放在一行就又是一个序列。

　　还有就是其实还是可以继续构造的。

　　最后就是原题的代码：

　　

#include <cstdio>
const int maxf=+;
long long jl1[][];
int w[];
int ws(int a){
    int ans=;
    while(a){
        ans++;
        a/=;
    }
    return ans;
}
long long P(int len){
    long long ans=;
    for(int i=;i<=len;i++)
        ans*=(long long);
    return ans;
}
long long Cl(long long a){
    int len=;
    long long te=a;
    while(a){
        len++;
        w[len]=a%;
        a/=;
    }
    a=te;
    long long ans=;
    ans+=(a-P(len-)+)*len;//处理较大的
    for(int i=;i<=len-;i++)
        ans+=(P(i)-P(i-))*(long long)i;
    return ans;
}
long long Cl_(long long a){
        int len=;
    long long te=a;
    while(a){
        len++;
        w[len]=a%;
        a/=;
    }
    a=te;
    long long ans=;
    ans+=Cl(P(len-))*(a-P(len-)+)+((a-P(len-)+)*(a-P(len-))/(long long))*(long long)len;
    for(int i=;i<=len-;i++)
        ans+=Cl(P(i-))*(P(i)-P(i-))+((P(i)-P(i-))*(P(i)-P(i-)-)/(long long))*(long long)i;
    return ans;
}
int main(){
    int q;
    scanf("%d",&q);
    for(int i=;i<=q;i++){
        long long a;
        bool c=;
        scanf("%lld",&a);
        int l=,r=maxf;
        while(l<=r){
            int mid=(r-l)/+l;
            long long js=Cl_(mid);
            if(js==a){
                printf("%d\n",mid%);
                c=;
                break;
            }
            else if(js>a)
                r=mid-;
            else
                l=mid+;
        }//找到在哪个序列里
        a-=Cl_(r);
        l=,r=maxf;
        while(l<=r){
            int mid=(r-l)/+l;
            long long js=Cl(mid);
            if(js==a&&c){
                c=;
                printf("%d\n",mid%);
                break;
            }
            else if(js>a)
                r=mid-;
            else
                l=mid+;
        }
        a-=Cl(r);
        long long s=r+;//找到在哪个数上
        int len=;
        while(s){
            len++;
            w[len]=s%;
            s/=;
        }
        if(c)
            printf("%d\n",w[len-a+]);
    }
    return ;
}