Codeforces Round #649 (Div. 2) A. XXXXX (贪心)

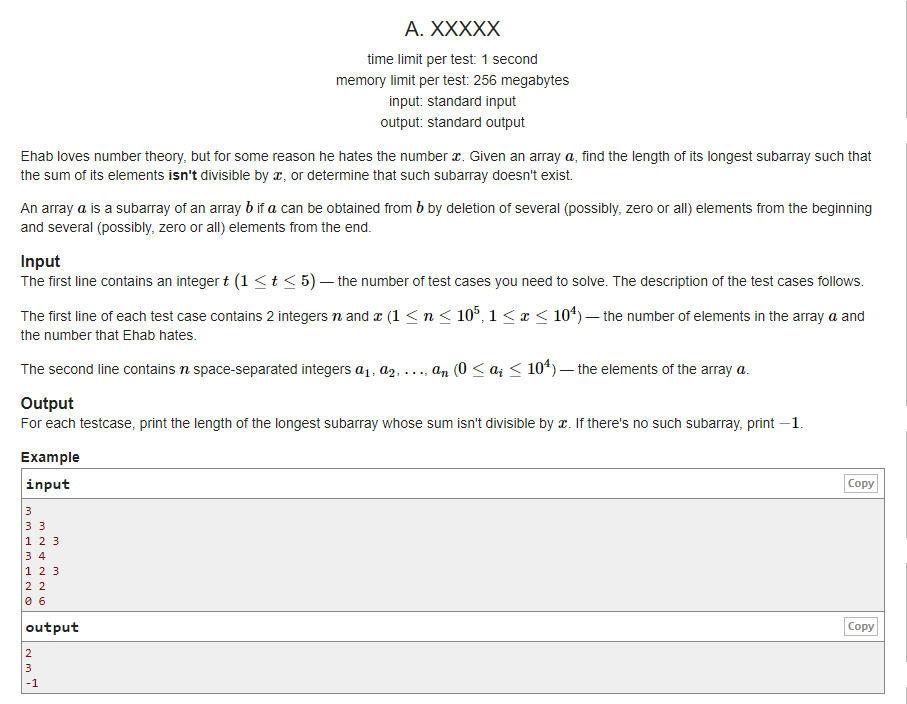
• 题意:有一个长度为\(n\)的数组,找一段最长子数组,使得其元素和为\(x\),如果存在,输出子数组的长度,否则输出\(-1\).

• 题解:这题我们要从元素和\(sum\)来考虑,首先,如果原数组的所有元素都被\(x\)整除,那么条件不成立.

  ​ 假如原数组的\(sum\)不被\(x\)整除,那么长度就为\(n\),如果被\(x\)整除,那么我们贪心来想,从前和从后来找第一个\(a[i]\)%\(x\ne0\)的位置,然后比较求个最长即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  const int INF = 0x3f3f3f3f;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<ll,ll> PLL;
  
  int t;
  int n,x;
  int a[N];
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>t;
  	 while(t--){
  	 	int sum=0;
  	 	bool ok=0;
  	 	cin>>n>>x;
  	 	 for(int i=1;i<=n;++i){
  	 	 	cin>>a[i];
  	 	 	sum+=a[i];
  	 	 	if(a[i]%x!=0) ok=1;
  	 	 }
  	 	  if(!ok){
  	 	 	cout<<-1<<endl;
  	 	 	continue;
  	 	 }
  	 	 if(sum%x!=0){
  	 	 	cout<<n<<endl;
  	 	 	continue;
  	 	 }
  	 	 int f=n;
  	 	 int b=0;
  	 	 for(int i=1;i<=n;++i){
  	 	 	if(a[i]%x!=0){
  	 	 		f=i;
  	 	 		break;
  	 	 	}
  	 	 }
  	 	 for(int i=n;i>=1;--i){
  	 	 	if(a[i]%x!=0){
  	 	 		b=i;
  	 	 		break;
  	 	 	}
  	 	 }
  	 	 cout<<max(n-f,b-1)<<endl;
  	 }
  
      return 0;
  }