矩阵的基本性质 之 对称矩阵,Hermite矩阵,正交矩阵,酉矩阵
1.对称矩阵

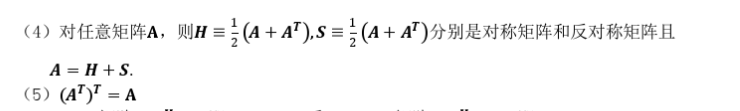
2.Hermite矩阵

3.正交矩阵

4.酉矩阵

矩阵的基本性质 之 对称矩阵,Hermite矩阵,正交矩阵,酉矩阵的更多相关文章
- Hermite 矩阵及其特征刻画
将学习到什么 矩阵 \(A\) 与 \(\dfrac{1}{2}(A+A^T)\) 两者生成相同的二次型,而后面那个矩阵是对称的,这样以来,为了研究实的或者复的二次型,就只需要研究由对称矩阵生成的二次 ...
- 对称矩阵、Hermite矩阵、正交矩阵、酉矩阵、奇异矩阵、正规矩阵、幂等矩阵
2016-01-27 21:03 524人阅读 评论(0) 收藏 举报 分类: 理论/笔记(20) 版权声明:本文为博主原创文章,转载请注明出处,谢谢! 题目:对称矩阵.Hermite矩阵.正交矩阵. ...
- Hermite 矩阵的特征值不等式
将要学习 关于 Hermite 矩阵的特征值不等式. Weyl 定理 以及推论. Weyl 定理 Hermann Weyl 的如下定理是大量不等式的基础,这些不等式要么涉及两个 Hermite 矩 ...
- 矩阵快速幂——将运算推广到矩阵上HDU 1575
/* 本题的思路比较简单,就是将递推公式写出来,然后表达成为一个矩阵的形式 最后通过计算就可以得到一个符合题目要求的矩阵, 然后就是将矩阵上面所有的对角线元素相加 得到的结果即为所求的目标 */ #i ...
- 编程计算2×3阶矩阵A和3×2阶矩阵B之积C。 矩阵相乘的基本方法是: 矩阵A的第i行的所有元素同矩阵B第j列的元素对应相乘, 并把相乘的结果相加,最终得到的值就是矩阵C的第i行第j列的值。 要求: (1)从键盘分别输入矩阵A和B, 输出乘积矩阵C (2) **输入提示信息为: 输入矩阵A之前提示:"Input 2*3 matrix a:\n" 输入矩阵B之前提示
编程计算2×3阶矩阵A和3×2阶矩阵B之积C. 矩阵相乘的基本方法是: 矩阵A的第i行的所有元素同矩阵B第j列的元素对应相乘, 并把相乘的结果相加,最终得到的值就是矩阵C的第i行第j列的值. 要求: ...
- hermite矩阵
在读线代书.因为之前并没有上过线性代数的课.所以决定把基础打牢牢. 读书的时候当然会出现不懂的概念和术语或者定理什么的.所以在这记录一下啦--- hermit矩阵要理解它好像先要知道什么是共轭(con ...
- BZOJ 3240([Noi2013]矩阵游戏-费马小定理【矩阵推论】-%*s-快速读入)
3240: [Noi2013]矩阵游戏 Time Limit: 10 Sec Memory Limit: 256 MB Submit: 123 Solved: 73 [ Submit][ St ...
- (十进制高速幂+矩阵优化)BZOJ 3240 3240: [Noi2013]矩阵游戏
题目链接: http://www.lydsy.com/JudgeOnline/problem.php?id=3240 3240: [Noi2013]矩阵游戏 Time Limit: 10 Sec M ...
- Luogu P3390 【模板】矩阵快速幂&&P1939 【模板】矩阵加速(数列)
补一补之前的坑 因为上次关于矩阵的那篇blog写的内容太多太宽泛了,所以这次把一些板子和基本思路理一理 先看这道模板题:P3390 [模板]矩阵快速幂 首先我们知道矩阵乘法满足结合律而不满足交换律的一 ...
随机推荐
- laravel模板使用
{{ $var }} - 打印内容 {{ $var or 'default' }} - 打印内容并带一个默认值 {{{ $var }}} - 打印转义内容 {{-- Comment --}} - 注释 ...
- Quartz.Net系列(六):Quartz五大构件Trigger之TriggerBuilder解析
所有方法图: 1.Create.Build Create:创建一个TriggerBuilder Build:生成Trigger var trigger = TriggerBuilder.Create( ...
- linux网络编程-socket(2)
当客户端调用close函数的时候,服务器的read函数读到的数据是0读到文件结束通知,表示对端关闭了tcp连接 我们现实实现下面的功能: 1.tcp客户端从标准的输入流中得到输入数据发送到服务器,服务 ...
- Python3-random模块-生成伪随机数
Python3中的random模块可以生成一个伪随机数 常用的就三个模块函数 random.random() 返回0-1之间的一个随机数 random.randrange(i, j) 返回一个随机数 ...
- Spring Bean各阶段生命周期的介绍
一.xml方式配置bean 二.Aware接口 2.1 BeanNameAware 2.2 BeanFactoryAware 2.3 ApplicationContextAware 2.4 Aware ...
- Codeforces Round #652 (Div. 2) 总结
A:问正n边形的一条边和x轴平行的时候有没有一条边和y轴重合,直接判断n是否是4的倍数 #include <iostream> #include <cstdio> #inclu ...
- Python实用笔记 (23)面向对象高级编程——使用__slots__
正常情况下,当我们定义了一个class,创建了一个class的实例后,我们可以给该实例绑定任何属性和方法,这就是动态语言的灵活性.先定义class: class Student(object): pa ...
- 第一步:安装centos_8
关于centos的安装其实大部分时候都是在虚拟机环境下安装. 好处无疑有这几个:方便,快速,主要就是整出事情了我可以直接删了重装 我这边是在vmware下进行一个安装 vmware我这边给出下载链接: ...
- 使用Xmanager连接linux,操作“xhost +”时出现类似“xhost: unable to open display "192.168.1.1811:1.0" ”问题的解决
远程连接linux服务器时,有的时候需要把服务器上的图形界面投影到本地来进一步操作,比如linux下安装oracle时就需要在oracle用户下允许视图状态投影到本地,这需要使用命令: xhost + ...
- tableau入门学习笔记--分页功能
最近在使用tableau来制作报表,对于tableau也是第一次接触并使用,每天学习些新的功能来记录在博客里,给他人方便,也给自己方便 tableau分页功能 很多时候由于工作表过长而出现拖拽条,如果 ...

