2020牛客暑期多校训练营（第一场）H Minimum-cost Flow

Minimum-cost Flow

题目：给n个点，m条边。接下来m行包含（a,b,c），即a,b之间有单位流量代价为c的边。接下来有q个问题，每个问题给定（x，y），即假设每条边的容量为x/y时，从点1到点n流1单位的流量，最少的花费是多少，如果无法从点1到点n流1单位的流量则输出“NaN”。

思路：首先我们需要想到一个结论，每条边最多只能使用一次，这个自己比划一下就可以，其中包含贪心的想法。得到这个结论后，我们发现整张图就变成了流量为1的网络流。然后，根据（x，y）说明我们至少需要 y / x + (y % x != 0)条从1到n的最少花费路径，这个我们可以通过最小费用流预处理得到所有能够得到的最小花费路径，并记录每条路径的最小花费。这样，对于每个询问（x，y），我们只需要取前y / x小的边，如果y % x ！= 0，则从后面的边补充一些即可。

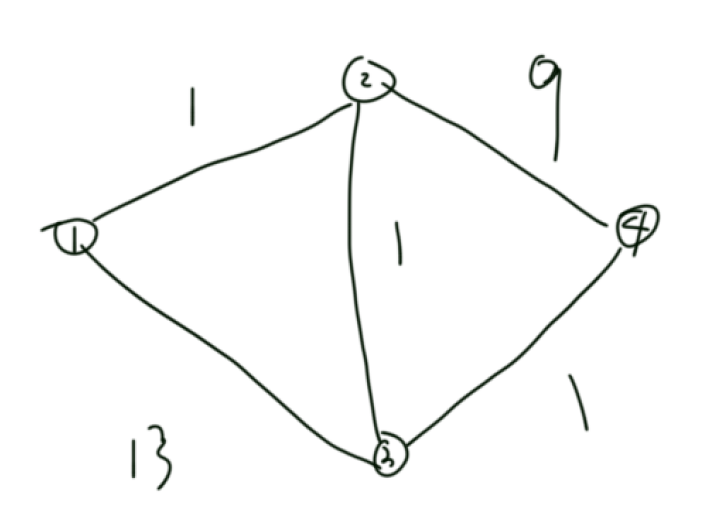
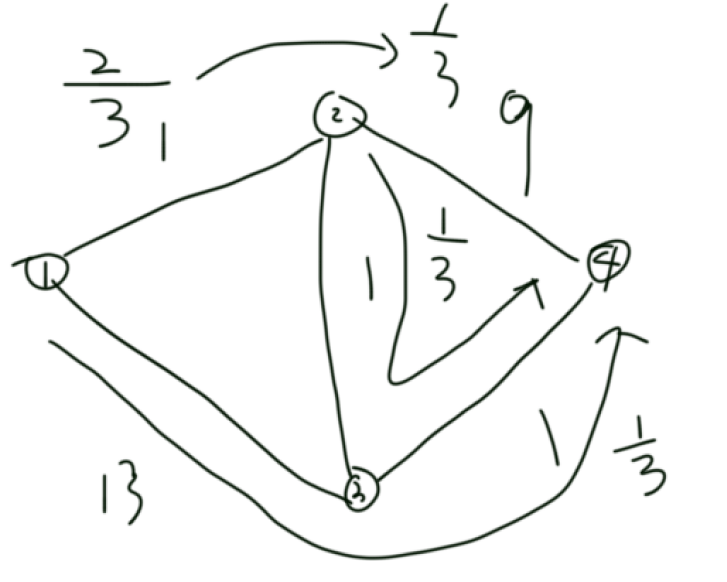
补充：为什么我们可以直接这样直接取路径，看上图，我们得到的最小花费应该是两个：3，21。这是懂得网络流算法都能看出的，如果我们有组询问（2,3），我们可以得到答案应该是ans = 3 * 2/3 + 21 * 1/3 = 9。但这两条路分别是1->2->3->4和1->3->2->4得到的，会感觉有点奇怪“这样就是答案”。其实我们需要回到网络流的反向边在算法中的用途"反流"和正向边可以把"反流"失去的流量再"补流"，下面附一个来体现ans = 9是怎么得到的，然后思考。

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <queue>
 #include <vector>
 #include <cstring>

 using namespace std;

 #define ll long long
 #define pb push_back
 #define fi first
 #define se second

 const int N = ;
 const int M = ;
 const int INF = 1e9 + 7e8;
 struct edge
 {
     int to, nxt, cap, flow, w;
 }e[M << ];
 int head[N], d[N], vis[N], pre[N];
 queue<int > que;
 int  a[N], b[N];
 int n, m, tot, s, t, cnt;

 inline void add(int u, int v, int w)
 {
     e[tot].to = v; e[tot].w = w; e[tot].cap = ;
     e[tot].flow = ; e[tot].nxt = head[u]; head[u] = tot++;
     e[tot].to = u; e[tot].w = -w; e[tot].cap = ;
     e[tot].flow = ; e[tot].nxt = head[v]; head[v] = tot++;
 }

 bool spfa()
 {
     for(int i = ; i <= n; ++i) d[i] = INF, vis[i] = false, pre[i] = -;
     while(!que.empty()) que.pop();
     d[s] = ; vis[s] = true; pre[s] = -;
     que.push(s);
     //printf("s = %d  t = %d\n", s, t);
     while(!que.empty()){
         int now = que.front();
         que.pop();
         vis[now] = false;

         for(int o = head[now]; ~o; o = e[o].nxt){
             if(e[o].cap - e[o].flow && d[e[o].to] > d[now] + e[o].w){
                 d[e[o].to] = d[now] + e[o].w;
                 pre[e[o].to] = o;
                 if(!vis[e[o].to]){
                     vis[e[o].to] = true;
                     que.push(e[o].to);
                 }
             }
         }
     }
     if(pre[t] == -) return false;
     else return true;
 }

 void mcmf()
 {
     while(spfa()){
         int _min = INF;
         for(int o = pre[t]; ~o; o = pre[e[o ^ ].to]){
             _min = min(_min, e[o].cap - e[o].flow);
         }
         for(int o = pre[t]; ~o; o = pre[e[o ^ ].to]){
             e[o].flow += _min;
             e[o ^ ].flow -= _min;
         }
         //cout << _min << endl;
         //cout << "dis = " << d[t] << endl;
         a[++cnt] = d[t];
         //cout << "d = " << d[t] << endl;
     }
     for(int i = ; i <= cnt; ++i) a[i] += a[i - ];
 }

 ll GCD(ll a, ll b)
 {
     return b ==  ? a : GCD(b, a % b);
 }

 void solve()
 {
     while(~scanf("%d%d", &n, &m)){
         cnt = ;
         for(int i = ; i <= n; ++i) head[i] = -; tot = ;
         int x, y, w;
         for(int i = ; i <= m; ++i){
             scanf("%d%d%d", &x, &y, &w);
             add(x, y, w);
         }
         s = ; t = n;
         mcmf();

         int q;
         scanf("%d", &q);
         while(q--){
             int x, y;
             scanf("%d%d", &x, &y);
             if(x == ){
                 puts("NaN");
                 continue;
             }
             int gcd = GCD(x, y);
             y /= gcd; x /= gcd;

             int need = y / x + (y % x != );
             if(need > cnt){
                 puts("NaN");
                 continue;
             }

             need = y / x;
             ll up = (ll)a[need] * x;
             ll down = y;
             int remains = y % x;
             up += (ll)(a[need + ] - a[need]) * remains;
             gcd = GCD(up, down);
             up /= gcd; down /= gcd;
             printf("%lld/%lld\n", up, down);
         }
     }
 }

 int main(){

     solve();

     return ;
 }