重新点亮linux 命令树————二进制安装[十一八]
前言
简单介绍一下二进制安装
正文
wget https://openresty.org/download/openresty-1.15.8.1.tar.gz
tar -zxf openresty-VERSION.tar.gz
cd openresty-VERSION/
./configure --prefix=/usr/local/openresty 配置我们的系统安装位置
make -j2
make install
第一步进行下载:
第二三步进行解压并且进入:

第四步:
简单配置一下安装目录,这个是避免文件分散。
./configure --prefix=/usr/local/openresty
这个时候会包gc++缺少那么就应该安装一下。
错误:

解决:
然后再次执行上面的配置命令:
这样就成功了。所以一般在编译之前最好用configure 去检查一下。
第五部:
make -j2 这个时候就是进行编译了。j2的意思是使用两个逻辑cpu进行编译。
这时候就会进行大量的编译程序。

这个时候就会生成一个build文件进行查看。
第六个:make install 进行安装。

这样就安装完成了。
linux 命令树
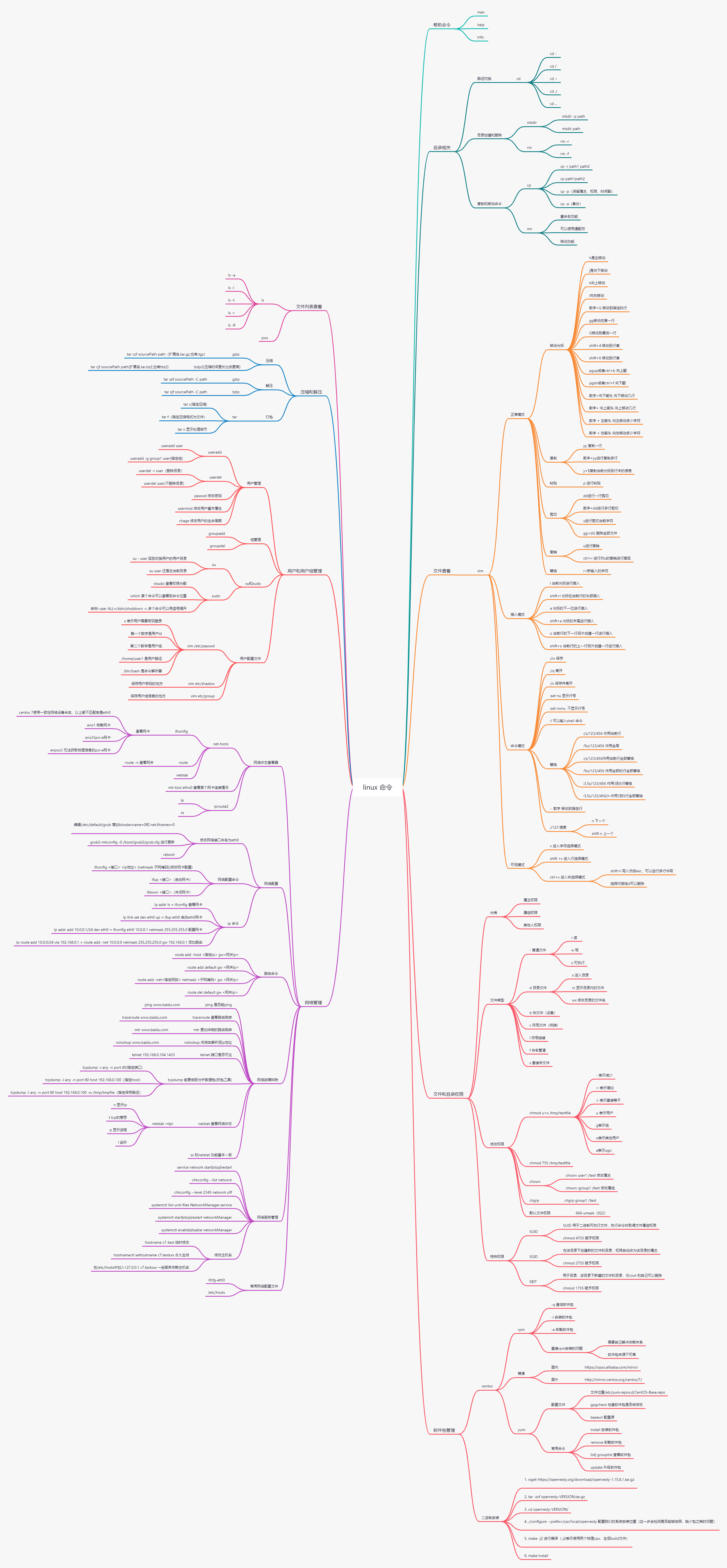
结
下一节grub配置文件
重新点亮linux 命令树————二进制安装[十一八]的更多相关文章
- 重新点亮linux 命令树————帮助命令[一]
前言 重新整理一下linux的命令. 正文 这里首先介绍帮助命令. 帮助命令常用的有三个: man help info 那么就来看下这三个. man 第一个man,man不是男人的意思,而是manua ...
- linux命令——mutt的安装和使用【转】
linux命令--mutt的安装和使用[转] 首先介绍一下mutt这个软件,它是一款基于文字界面的邮件客户端,非常小巧,但功能强大,可以用它来读写,回复保存和删除你的邮件,能在linux命令行模式下收 ...
- 在Linux命令行模式安装VMware Tools
在Linux命令行模式安装VMware Tools 方法/步骤1: 首先启动CentOS 7,在VMware中点击上方“VM”,点击“Install VMware Tools...”(如已安装则显示“ ...
- Linux中MySQL二进制安装步骤
MySQL二进制安装步骤 安装依赖环境 [root@node3 ~]# yum -y install libaio 将mysql-5.7.26-linux-glibc2.12-x86_64.tar.g ...
- Linux(CentOS7)下二进制安装MySQL5.7.26
记录一下自己在 CentOS7 下二进制安装 MySQL5.7.26 的过程,之前使用 Linux(CentOS7)下rpm安装MySQL8.0.16 之后发现 rpm 方式安装不利于维护,也不利于单 ...
- WebLogic 12c Linux 命令行 静默安装
CentOS 6.3安装配置Weblogic 10 http://www.linuxidc.com/Linux/2014-02/96918.htm Oracle WebLogic 11g 安装部署文 ...
- Linux命令之rpm安装命令
在 Linux 操作系统下,几乎所有的软件均通过RPM 进行安装.卸载及管理等操作.RPM 的全称为Redhat Package Manager ,是由Redhat 公司提出的,用于管理Linux 下 ...
- linux命令模式配置安装mysql
系统环境: centos 7.1 使用模式:命令模式 使用工具:xshell5 . xftp5 安装mysql前必须删除干净旧的安装包和残留文件,否则安装会失败 查看旧的安装包 rpm -qa | g ...
- 【Linux 命令】iftop安装与简单使用
iftop是linux下的一个流量监控工具,用于查看实时网络流量,反向解析IP,显示端口信息官网:http://www.ex-parrot.com/~pdw/iftop/ 1.安装必须软件包 yum ...
- MySQL在linux上的二进制安装方法
建组.建用户: [root@dbking mysql]# groupadd mysql [root@dbking mysql]# useradd -g mysql mysql 解压安装程序: [roo ...
随机推荐
- Codeforces Round 734 (Div. 3)B2. Wonderful Coloring - 2(贪心构造实现)
思路: 分类讨论: 当一个数字出现的次数大于等于k,那么最多有k个能被染色, 当一个数字出现的次数小于k,南那么这些数字都可能被染色 还有一个条件就是需要满足每个颜色的数字个数一样多,这里记出现次数小 ...
- Ansible 基础入门
2)Ansible 介绍 Ansible 基本概念 Ansible 是一种自动化运维工具,基于 Paramiko 开发的,并且基于模块化工作,Ansible 是一种集成 IT 系统的配置管理.应用部署 ...
- [.Net]使用Soa库+Abp搭建微服务项目框架(二):面向服务体系的介绍
上一章我们建立了一个典型的面向领域设计的Abp小项目,如果按照常规的开发方式,会遇到什么问题呢? 先来完善一下这个小项目,在定义好各实体类后,运行Miguration并向数据库里写入一些初始数据. ...
- tag 转 分支 branch
获得最新 git fetch origin 获取tag git tag tag 转 branch git branch newbranch vtest.1.0.FINAL --- git branch ...
- gap 单词学习 对标 open
为什么gap 和 open 联系记忆呢? gap是从行为动作中来 open 中 op 就是 up,是从 单词字母的角度来 但是 本意 这两个单词都差不多 gap gap : 来自PIE*ghai,打呵 ...
- Navicat 通过 Http通道 连接远程 Mysql
https://jingyan.baidu.com/article/3d69c551aa54dff0cf02d7a0.html 注意本机ip填写 localhost
- Android Studio导出APP的数据库db文件
原文地址:Android Studio导出APP的数据库db文件 | Stars-One的杂货小窝 最近项目开发需要使用到Android内置的Sqlite存数据,但是公司里没有对应的调试环境,只能让现 ...
- .NET开源快速、强大、免费的电子表格组件
前言 今天大姚给大家分享一个.NET开源(MIT License).快速.强大.免费的电子表格组件,支持数据格式.冻结.大纲.公式计算.图表.脚本执行等.兼容 Excel 2007 (.xlsx) 格 ...
- 崩溃bug日志总结2
目录介绍 1.1 java.lang.ClassNotFoundException类找不到异常 1.2 java.util.concurrent.TimeoutException连接超时崩溃 1.3 ...
- App启动流程
目录介绍 1.什么是Zygote进程 1.1 简单介绍 1.2 各个进程的先后顺序 1.3 进程作用说明 2.Zygote进程的启动流程 2.1 源码位置 2.2 ZygoteInit类的main方法 ...
