[C++]线段树 区间查询 单点修改

线段树 区间查询 单点修改

算法思想

这个算法是用于数组的查询和修改

可以高效的进行查询修改

但是会增加内存的使用

本质上是一种 空间换时间 的算法

这个算法把一串数组无限二分

直到分的只剩下一个数据

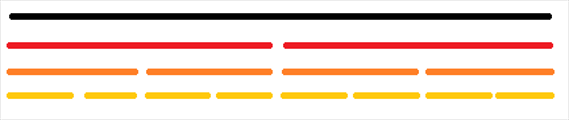
将每一段看成一个节点

这样就组成了一个树形结构

故名 线段树

代码实现

实现这个代码一共分三个步骤：

建树 查询 修改

这里先把变量含义解释一遍：

#define maxn 1000010
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
/*
	mid 线段中间节点的小标
	li i线段的左子树
	ri i线段的右子树
*/

int n,val[maxn];
/*
	n 数组的长度
	val 数组的值
*/

struct Node{
	int l,r,sum;
}tree[maxn];
/*
	tree 即这个树形结构
	tree[i].l i线段的左端
	tree[i].r i线段的右端
	tree[i].sum i线段的所有节点的权值和
*/

建树

void build(int i,int l,int r){
	tree[i].l = l;
	tree[i].r = r;
	if(l == r){
		tree[i].sum = val[l];
		return ;
	}
	build(li,l,mid);
	build(ri,mid+1,r);
	tree[i].sum = tree[li].sum + tree[ri].sum;
	return ;
}

欲建树 先分步

我们只要处理好每个节点的三个值(l,r,sum)

这棵树自然也就建好了

l,r直接赋值即可

如果 if(l == r)

则说明这个节点已经无法再二分了

那么就把 \(val\) 的值直接赋给 \(sum\)

并且要记得 return ;

若 \(l != r\)

那就继续二分建子树

然后再把两个子树的值加起来即为自己的 \(sum\)

查询

int search(int i,int l,int r){
	if(l <= tree[i].l && tree[i].r <= r)
		return tree[i].sum;
	if(tree[i].r < l || r < tree[i].l)
		return 0;

	int ans = 0;
	if(tree[li].r >= l) ans += search(li,l,r);
	if(tree[ri].l <= r) ans += search(ri,l,r);
	return ans;
}

这步的主要思想是能大块就返回大块的值

不能再二分给儿子线段处理

由于已经把数组分得很细

因此不存在查询边界在线段中却无法二分的情况

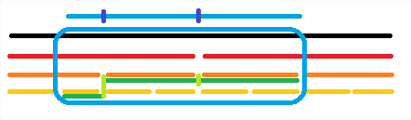
• \(l <= tree[i].l\) && \(tree[i].r <= r\)

这说明线段已经完全包裹在区间内(就和第二根绿色线段一样)

直接返回这个线段的值即可

• \(tree[i].r < l\) \(||\) \(r < tree[i].l\)

这说明线段完全不在取值区间内

那就返回0

• \(tree[li].r >= l\)

这说明有区间一部分在左子线段上

那就二分进行搜索

然后返回搜好的值

• \(tree[ri].l <= r\)

和上面同理

有区间一部分在右子线段上

修改

void add(int i,int dis,int k){
	if(tree[i].l == tree[i].r){
		tree[i].sum += k;
		return ;
	}
	if(dis <= tree[li].r)
		add(li,dis,k);
	else
		add(ri,dis,k);
	tree[i].sum = tree[li].sum + tree[ri].sum;
	return ;
}

修改我自身感觉和建树有点相像

就是改变一个节点的值然后再将涉及到这个节点的线段重新建树

• \(tree[i].l == tree[i].r\)

这代表已经找到了这个节点

那就把这个点的值修改掉

• \(dis <= tree[li].r\)

如果在线段里

那就继续找

• \(tree[i].sum = tree[li].sum + tree[ri].sum;\)

更新线段的值

线段数 区间修改 单点查询

Code

#include<bits/stdc++.h>
#define maxn 1000010
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
using namespace std;

int n,val[maxn];

struct Node{
	int l,r,sum;
}tree[maxn];

void Read(){
	cin >> n;
	for(int i = 1;i <= n;i++)cin >> val[i];
}

void build(int i,int l,int r){
	tree[i].l = l;
	tree[i].r = r;
	if(l == r){
		tree[i].sum = val[l];
		return ;
	}
	build(li,l,mid);
	build(ri,mid+1,r);
	tree[i].sum = tree[li].sum + tree[ri].sum;
	return ;
}

int search(int i,int l,int r){
	if(l <= tree[i].l && tree[i].r <= r)
		return tree[i].sum;
	if(tree[i].r < l || r < tree[i].l)
		return 0;

	int ans = 0;
	if(tree[li].r >= l) ans += search(li,l,r);
	if(tree[ri].l <= r) ans += search(ri,l,r);
	return ans;
}

void add(int i,int dis,int k){
	if(tree[i].l == tree[i].r){
		tree[i].sum += k;
		return ;
	}
	if(dis <= tree[li].r)
		add(li,dis,k);
	else
		add(ri,dis,k);
	tree[i].sum = tree[li].sum + tree[ri].sum;
	return ;
}

void interaction(){
	while(1){
		int tot;
		cin >> tot;
		if(tot == 1){
			int l,r;
			cin >> l >> r;
			cout << search(1,l,r) << endl;
		} else if(tot == 2){
			int dis,k;
			cin >> dis >> k;
			add(1,dis,k);
		} else if(tot == 3){
			return ;
		}
	}
}

int main(){
	cout << "query section" << endl << "change point" << endl;
	Read();
	build(1,1,n);
	cout << "query 1" << endl << "change 2" << endl << "break 3" << endl;
	interaction();
	return 0;
}