【LeetCode二叉树#01】二叉树的遍历（递归/迭代）

二叉树递归遍历

写递归算法时候需要遵循的三个点：

1. 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
2. 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
3. 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

前序遍历

以前序遍历为例

LeetCode上的代码模板如下：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {

    }
};

因为要使用递归，所以肯定得有一个递归函数，那么现在按照上面的三个规则来写

1、确定递归函数的参数和返回值：因为要打印出前序遍历节点的数值，所以参数里需要传入vector来放节点的数值，除了这一点就不需要再处 理什么数据了也不需要有返回值，所以递归函数返回类型就是void，代码如下：

void traversal(TreeNode* cur, vector<int>& vec){

}

2.确定终止条件：在递归的过程中，如何算是递归结束了呢，当然是当前遍历的节点是空了，那么本层递归就要结束了，所以如果当前遍历的这个节点是空，就直接return，代码如下：

void traversal(TreeNode* cur, vector<int>& vec){
    if(cur == NULL) return;
}

3.确定单层递归的逻辑：前序遍历是中左右的循序，所以在单层递归的逻辑，是要先取中节点的数值，代码如下：

void traversal(TreeNode* cur, vector<int>& vec){
    if(cur == NULL) return;
    vec.push_back(cur->val);//取出当前节点的值(中)
    traversal(cur->left, vec);//到左子树的节点中取值(左)
    traversal(cur->right, vec);//到右子树的节点中取值(右)
}

因此，前序遍历的完整代码如下：

class Solution {
public:
    //编写递归函数
	void traversal(TreeNode* cur, vector<int>& vec){
		if(cur == NULL)return;
        vec.push_back(cur->val);//取出当前节点的值
        traversal(cur->left, vec);//到左子树的节点中取值
        traversal(cur->right, vec);//到右子树的节点中取值
	}
    vector<int> preorderTraversal(TreeNode* root) {
		//定义结果数组
        vector<int> res;
        traversal(root, res);
        return res;
    }
};

中序遍历

同理，中序和后序遍历中只需修改递归函数traversal中的单层递归逻辑即可

class Solution {
public:
	void traversal(TreeNode* cur, vector<int>& vec){
		if(cur == NULL)return;
        traversal(cur->left, vec);//到左子树的节点中取值(左)
        vec.push_back(cur->val);//取出当前节点的值(中)
        traversal(cur->right,vec);//到右子树的节点中取值(右)

	}
    vector<int> inorderTraversal(TreeNode* root) {
		//定义结果数组
        vector<int> res;
        traversal(root, res);
        return res;
    }
};

后序遍历

class Solution {
public:
    //编写递归函数
    void traversal(TreeNode* cur, vector<int>& vec){
        if(cur == NULL) return;
        traversal(cur->left, vec);
        traversal(cur->right, vec);
        vec.push_back(cur->val);

    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        traversal(root, res);
        return res;
    }
};

注意

前/中/后序遍历的顺序里，所谓的“中”（例如中左右）其实可以理解为在使用递归三部曲时的“确认单层逻辑”的过程

二叉树非递归遍历

面试时有可能会考察一些简单的递归逻辑的迭代法实现

例如，用迭代法来实现前中后序遍历

前序遍历（迭代法）

图示模拟

通过迭代法进行前序遍历主要是利用栈的方式实现的

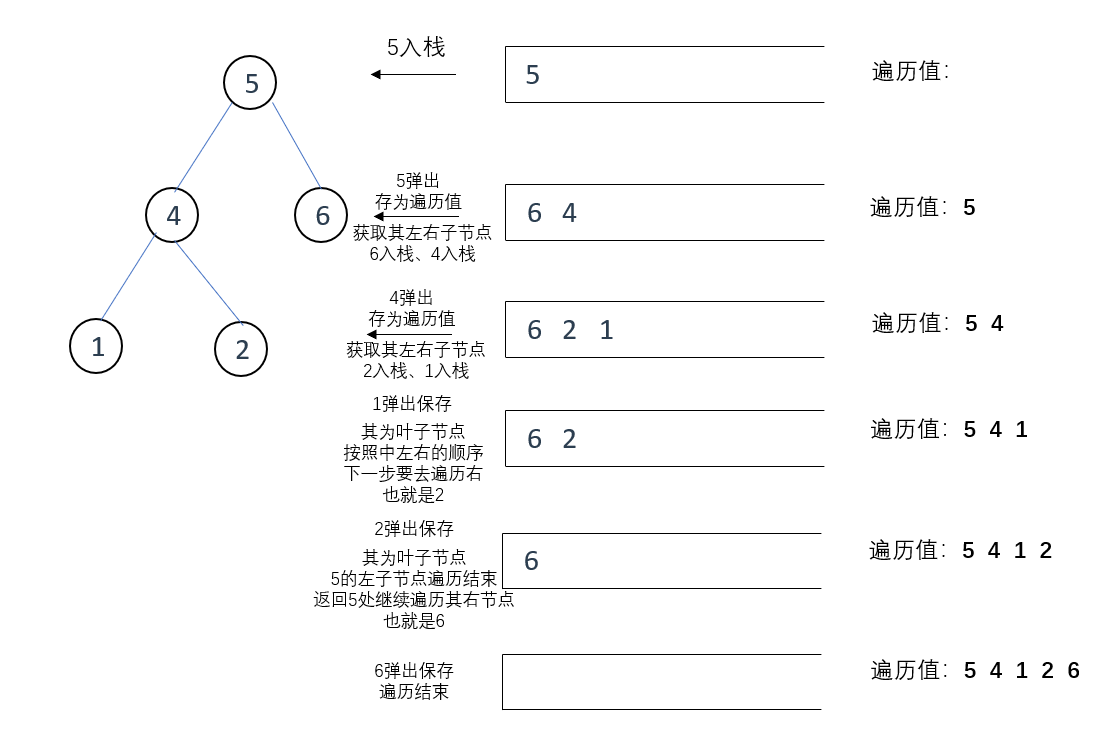
如图所示，将当前遍历到的节点存入栈中，保存其值到结果数组后将其弹出，然后根据该节点的左右指针，把该节点的左右子节点再放入栈中

注意：放入栈的顺序要与遍历顺序相反

例如：前序遍历的顺序是 中左右 ，当 5 入栈时实际上是在进行对于 中 的遍历，而 5 的左右子节点入栈时要以 “右左” 的顺序进入，这样在出栈时才能保证顺序为 “左右” ，才能达成 "中左右" 的遍历顺序

代码

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
		//定义一个栈，注意保存的是节点数据类型
        stack<TreeNode*> st;
        //定义一个结果数组
        vector<int> res;
        //检测传入节点是否为空
        if(root == NULL) return res;
        //将根节点压栈
        st.push(root);                           //中
        //当栈中不为空时持续遍历
        while(!(st.empty())){
            //保存当前栈顶节点
            TreeNode* node = st.top();
            //弹出当前节点
            st.pop();
            //保存结果
            res.push_back(node->val);
            //判断当前节点有无左右子节点，有就按顺序压栈（明确你的出栈顺序，入栈时要相反）
            if(node->right)st.push(node->right); //右
            if(node->left)st.push(node->left);   //左
        }
        return res;//最终遍历结果的顺序：中左右（前序）
    }
};

后序遍历（迭代法）

因为中序遍历的迭代法不是简单的在前序的基础上修改顺序就可以实现的，所以先说后续遍历

在前序的基础上实现后序的方式很巧妙

后序遍历顺序：左右中

前序遍历顺序：中左右

因为要使用栈来实现迭代遍历，所以在实际代码中前序遍历的入栈顺序是：中右左

此时我们对其进行一个翻转处理，是不是就变成了左右中，即后序遍历的顺序

代码

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
		//定义一个栈，注意保存的是节点数据类型
        stack<TreeNode*> st;
        //定义一个结果数组
        vector<int> res;
        //检测传入节点是否为空
        if(root == NULL) return res;
        //将根节点压栈
        st.push(root);                           //中
        //当栈中不为空时持续遍历
        while(!(st.empty())){
            //保存当前栈顶节点
            TreeNode* node = st.top();
            //弹出当前节点
            st.pop();
            //保存结果
            res.push_back(node->val);
            //判断当前节点有无左右子节点，有就按顺序压栈（明确你的出栈顺序，入栈时要相反）
            if(node->left)st.push(node->left);   //左
            if(node->right)st.push(node->right); //右
            //出栈顺序：中右左(与入栈相反)
        }
        //翻转数组
        reverse(res.begin(), res.end());
        return res;//最终遍历结果的顺序：左右中（后序）
    }
};

中序遍历（迭代法）

通过前序和后序遍历的实现可以发现，这个过程其实可以分为遍历节点和处理节点两部分

并且在前序和后序遍历中，要遍历的节点与要处理的节点为同一顺序，因此可以按照上面的模式写出代码

但是，中序遍历的过程中，遍历和处理节点并不能够同时进行（顺序不一致），因此需要新的实现逻辑

中序遍历的动画如下：

首先，中序遍历的顺序是 左中右

因此从头结点 5 开始，我们定义一个指针一直遍历该二叉树的左指针指向的节点（左子节点）并压栈，直到指针指向空

然后开始从栈顶取节点

此时取的肯定是叶子节点，但是我们仍要判断其是否有左右节点（显然是没有的，要不然上面的指针也不会指向空）

将该节点的值保存到结果数组中，重复上述操作

代码

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
		//定义栈
        stack<TreeNode*> st;
        vector<int> res;
        //将指针指向根节点
        TreeNode* cur = root;
        //遍历
        while(!(st.empty()) || cur ! = NULL){
            //判断是否遍历到最底层
            if(cur ! = NULL){
                st.push(cur);//压栈
                cur = cur->left;//继续向左遍历
            }else{//当遍历到了左边的最底层，开始出栈（处理数据，即放进res）
                cur = st.top();//让指针指向当前弹出的节点
                st.pop();
                res.push_back(cur->val);
                //判断每个出栈的节点是否有左右子节点
                cur = cur->right;//如果有，则又会触发if的第一个条件，继续将右子节点压栈
                //不存在的话cur指向空就右来到else这
            }
        }
        return res;
    }
};