神经网络之卷积篇：详解卷积神经网络示例（Convolutional neural network example）

详解卷积神经网络示例

假设，有一张大小为32×32×3的输入图片，这是一张RGB模式的图片，想做手写体数字识别。32×32×3的RGB图片中含有某个数字，比如7，想识别它是从0-9这10个数字中的哪一个，构建一个神经网络来实现这个功能。

用的这个网络模型和经典网络LeNet-5非常相似，灵感也来源于此。LeNet-5是多年前Yann LeCun创建的，所采用的模型并不是LeNet-5，但是受它启发，许多参数选择都与LeNet-5相似。输入是32×32×3的矩阵，假设第一层使用过滤器大小为5×5，步幅是1，padding是0，过滤器个数为6，那么输出为28×28×6。将这层标记为CONV1，它用了6个过滤器，增加了偏差，应用了非线性函数，可能是ReLU非线性函数，最后输出CONV1的结果。

然后构建一个池化层，这里选择用最大池化，参数\(f=2\)，\(s=2\)，因为padding为0，就不写出来了。现在开始构建池化层，最大池化使用的过滤器为2×2，步幅为2，表示层的高度和宽度会减少一半。因此，28×28变成了14×14，通道数量保持不变，所以最终输出为14×14×6，将该输出标记为POOL1。

人们发现在卷积神经网络文献中，卷积有两种分类，这与所谓层的划分存在一致性。一类卷积是一个卷积层和一个池化层一起作为一层，这就是神经网络的Layer1。另一类卷积是把卷积层作为一层，而池化层单独作为一层。人们在计算神经网络有多少层时，通常只统计具有权重和参数的层。因为池化层没有权重和参数，只有一些超参数。这里，把CONV1和POOL1共同作为一个卷积，并标记为Layer1。虽然在阅读网络文章或研究报告时，可能会看到卷积层和池化层各为一层的情况，这只是两种不同的标记术语。一般在统计网络层数时，只计算具有权重的层，也就是把CONV1和POOL1作为Layer1。这里用CONV1和POOL1来标记，两者都是神经网络Layer1的一部分，POOL1也被划分在Layer1中，因为它没有权重，得到的输出是14×14×6。

再为它构建一个卷积层，过滤器大小为5×5，步幅为1，这次用10个过滤器，最后输出一个10×10×10的矩阵，标记为CONV2。

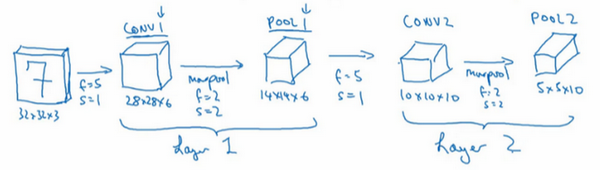
然后做最大池化，超参数\(f=2\)，\(s=2\)。大概可以猜出结果，\(f=2\)，\(s=2\)，高度和宽度会减半，最后输出为5×5×10，标记为POOL2，这就是神经网络的第二个卷积层，即Layer2。

如果对Layer1应用另一个卷积层，过滤器为5×5，即\(f=5\)，步幅是1，padding为0，所以这里省略了，过滤器16个，所以CONV2输出为10×10×16。看看CONV2，这是CONV2层。

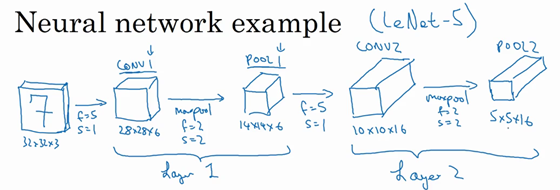
继续执行做大池化计算，参数\(f=2\)，\(s=2\)，能猜到结果么？对10×10×16输入执行最大池化计算，参数\(f=2\)，\(s=2\)，高度和宽度减半，计算结果猜到了吧。最大池化的参数\(f=2\)，\(s=2\)，输入的高度和宽度会减半，结果为5×5×16，通道数和之前一样，标记为POOL2。这是一个卷积，即Layer2，因为它只有一个权重集和一个卷积层CONV2。

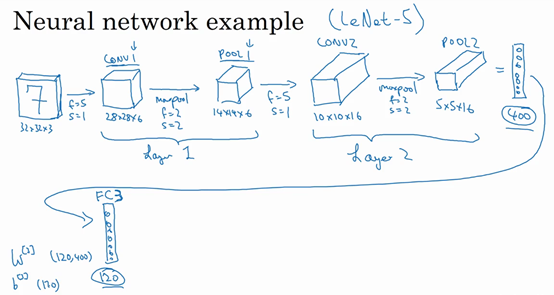
5×5×16矩阵包含400个元素，现在将POOL2平整化为一个大小为400的一维向量。可以把平整化结果想象成这样的一个神经元集合，然后利用这400个单元构建下一层。下一层含有120个单元，这就是第一个全连接层，标记为FC3。这400个单元与120个单元紧密相连，这就是全连接层。这是一个标准的神经网络。它的权重矩阵为\(W^{\left\lbrack 3 \right\rbrack}\)，维度为120×400。这就是所谓的“全连接”，因为这400个单元与这120个单元的每一项连接，还有一个偏差参数。最后输出120个维度，因为有120个输出。

然后对这个120个单元再添加一个全连接层，这层更小，假设它含有84个单元，标记为FC4。

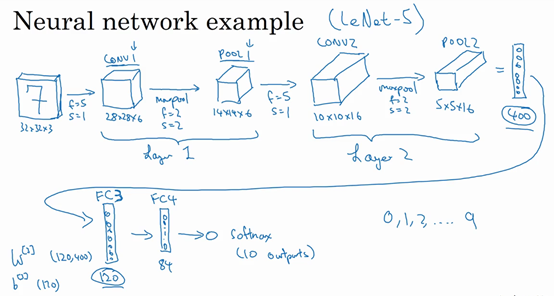
最后，用这84个单元填充一个softmax单元。如果想通过手写数字识别来识别手写0-9这10个数字，这个softmax就会有10个输出。

此例中的卷积神经网络很典型，看上去它有很多超参数，关于如何选定这些参数，后面提供更多建议。常规做法是，尽量不要自己设置超参数，而是查看文献中别人采用了哪些超参数，选一个在别人任务中效果很好的架构，那么它也有可能适用于自己的应用程序。

现在，想指出的是，随着神经网络深度的加深，高度\(n_{H}\)和宽度\(n_{W}\)通常都会减少，前面就提到过，从32×32到28×28，到14×14，到10×10，再到5×5。所以随着层数增加，高度和宽度都会减小，而通道数量会增加，从3到6到16不断增加，然后得到一个全连接层。

在神经网络中，另一种常见模式就是一个或多个卷积后面跟随一个池化层，然后一个或多个卷积层后面再跟一个池化层，然后是几个全连接层，最后是一个softmax。这是神经网络的另一种常见模式。

接下来讲讲神经网络的激活值形状，激活值大小和参数数量。输入为32×32×3，这些数做乘法，结果为3072，所以激活值\(a^{[0]}\)有3072维，激活值矩阵为32×32×3，输入层没有参数。计算其他层的时候，试着自己计算出激活值，这些都是网络中不同层的激活值形状和激活值大小。

有几点要注意，第一，池化层和最大池化层没有参数；第二卷积层的参数相对较少，之前提到过，其实许多参数都存在于神经网络的全连接层。观察可发现，随着神经网络的加深，激活值尺寸会逐渐变小，如果激活值尺寸下降太快，也会影响神经网络性能。示例中，激活值尺寸在第一层为6000，然后减少到1600，慢慢减少到84，最后输出softmax结果。发现，许多卷积网络都具有这些属性，模式上也相似。

神经网络的基本构造模块已经讲完了，一个卷积神经网络包括卷积层、池化层和全连接层。许多计算机视觉研究正在探索如何把这些基本模块整合起来，构建高效的神经网络，整合这些基本模块确实需要深入的理解。根据经验，找到整合基本构造模块最好方法就是大量阅读别人的案例。