UnionFind 并查集

简介

UnionFind 主要用于解决图论中的动态联通性的问题（对于输入的一系列元素集合，判断其中的元素是否是相连通的）。

以下图为例：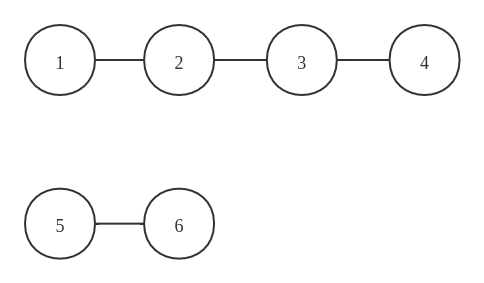

集合[1, 2, 3, 4] 和 [5, 6]中的每个元素之间都是相联通的，及 1 和 2、3、4都是连通的，而 1 和 5 则不是连通的。

UnionFind 主要的 API：

void union(int p, int q); 		// 将 p 和 q 连接起来
boolean connect(int p, int q);	// 判断 p 和 q 是否是相互连通的

这里的 “连通” 有以下性质：

• 自反性：p 和 p 自身是连通的
• 对称性：如果 p 和 q 是连通的，那么 q 和 p 也是连通的
• 传递性：如果 p 和 q 是连通，并且 q 和 r 是连通的，那么 p 和 r 也是联通的

实现

使用数组来存储连接的节点是一个可选的方案，使用数组 parent 来表示每个索引元素的直接连接节点，parent 的每个元素代表当前索引位置对应的元素的直接连接元素。

以上文的示例为例，初始时每个元素的连接情况如下图所示：

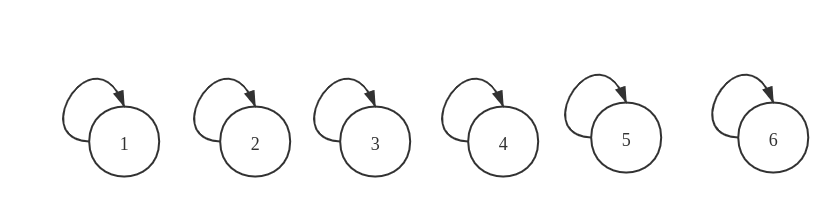
因为每个元素此时是没有与其他元素连接的，此时连接的元素就是它本身

此时的 parent 元素组成如下所示：

将 2 连接到 1、4 连接到 3、6 连接到5，连接起来，此时的连接情况如下所示：

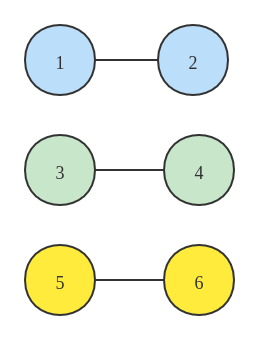
此时 parent 中的情况如下所示：

再将 3-4 连接到 1-2，此时的连接情况如下所示：

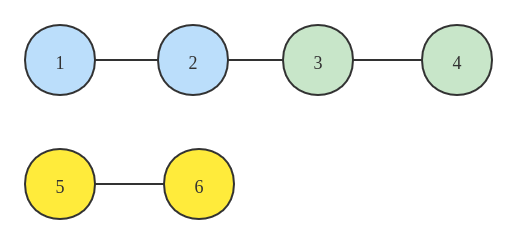
此时的 parent 中各个元素的对应的元素值如下所示：

这样就实现了刚开始举出的情况，现在，通过 parent就可以检测两个元素是否是“连”通的了。

具体的实现：

public class UnionFind {
    private final int[] parent; // 记录每个元素的连接信息
    private int count; // 用于记录当前的集合数量

    UnionFind(final int n) {
        parent = new int[n];
        count = n;

        // 初始化每个节点的父节点，使得每个节点连接到自身
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    /*
    	用于判断两个元素之间是否是连通的，
    	只要判断两个元素对应的根节点是否是一致的就可以判断两个节点是否是连通的
    */
    public boolean connect(int p, int q) {
        return find(p) == find(q);
    }

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);

        // 如果两个节点存在共同的根节点，那么它们就是连通的，不需要进行进一步的操作
        if (rootP == rootQ) return;

        parent[rootP] = rootQ; // 将 p 的根节点连接到 q 的根节点，这样 p 和 q 就是连通的
        count--;
    }

    public int count() {return count;}

    // 找到当前元素 p 的连接的根节点
    private int find(int p) {
        while (p != parent[p]) // 由于根节点不会存在连接到其它节点的情况，因此它连接的节点就是它本身
            p = parent[p];
        return p;
    }
}

实现优化

在上文提到的实现中，每次将两个不相连的节点进行连接操作，在最坏的情况下会导致这个集合成为一条链，从而每次的查找操作都需要在 \(O(n)\) 的时间复杂度内完成。以上文的初始集合为例，考虑以下的连接顺序：1->2、1->3、1->4、1->5、1->6，最后得到的结果如下图所示：

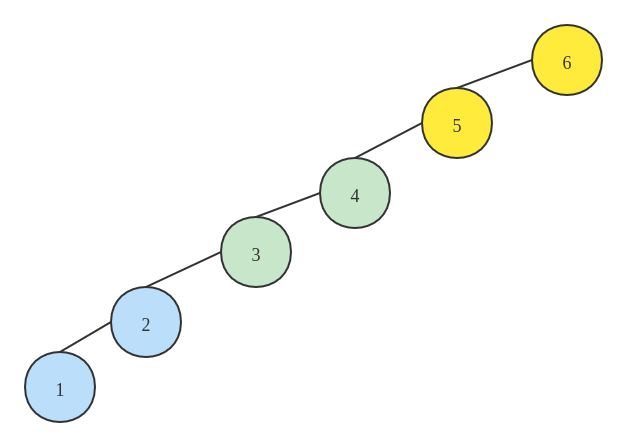
考虑这么一种情况，对于两个集合来讲，是将大集合连接到小集合得到的集合高度会小一些，还是将小集合连接到大集合得到的集合高度会小一些？以上文的例子为例，将 1-4 的集合连接到 5-6 的集合，得到的连接情况如下所示：

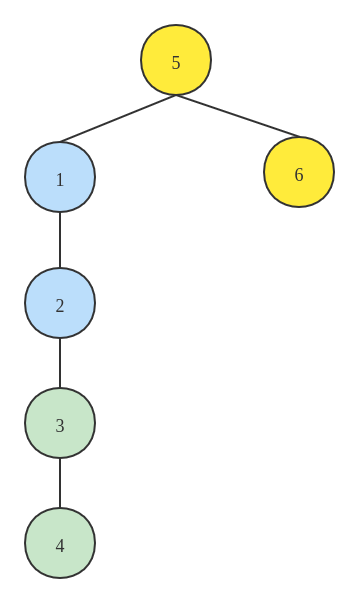
而如果将 5-6 的集合连接到 1- 4 的集合中，得到的连接情况如下所示：

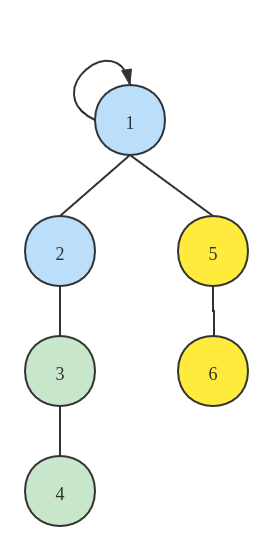
很明显，将 5-6 的集合插入到 1-4 中的高度更小，这是因为较大的集合有更多的位置容纳新连接的节点。因此，在连接时人为地将小集合连接到大集合可以有效地降低 UnionFind 每个操作的时间复杂度：

public class UnionFind {
    private final int[] parent;
    private final int[] sz; // 用于统计当前的元素包含的元素个数

    private int count;

    UnionFind(final int n) {
        parent = new int[n];
        sz = new int[n];
        count = n;

        for (int i = 0; i < n; ++i) {
            parent[i] = i;
            sz[i] = 1; // 每个节点在初始状态的时候集合的元素个数都是 1
        }
    }

    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);

        if (rootP == rootQ) return;

        // 将小集合连接到大集合，同时更新对应的集合元素个数
        if (sz[rootP] > sz[rootQ]) {
            parent[rootQ] = rootP;
            sz[rootP] += sz[rootQ];
        } else {
            parent[rootP] = rootQ;
            sz[rootQ] += sz[rootP];
        }

        count--;
    }
    // 省略部分代码
}

经过这么一顿操作之后，现在每个节点到根节点的高度为 \(logN\) ，相比较之前在最坏的情况下会生成一条链而形成 \(N\) 的高度，这种情况就要好很多了。

进一步的优化

实际上，上文给出的优化已经很好了，但是依旧存在可以优化的地方：将每个节点直接连接到根节点而不是父节点，可以进一步降低查找操作的时间复杂度。这中优化的方式也被称为 “路径压缩”，因为省去了向上查找根节点的操作。

// 其余代码同上

private int find(int p) {
    while (p != parent[p]) {
        // 更新当前的元素的父节点为父节点的父节点，因为根节点的父节点为它本身，因此最终会向上压缩一节高度
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

经过进一步的优化之后，理论上 UnionFind 的每个操作都为 \(O(1)\) 的时间复杂度，但是实际上使用“路径压缩”的方式进行优化并不会带来很大的性能提升。

实际使用

比较经典的一个实际使用是有关渗透阈值的估计，具体内容可以查看 https://coursera.cs.princeton.edu/algs4/assignments/percolation/specification.php