SP6779 GSS7

GSS7解题报告

前言

唔，有点恶心哪，废了两个多小时debug

思路

很容易看出傻子都知道，这个是树链剖分+线段树的裸题，只不过是恶心了点，这里重点讲一下细节问题

线段树

做过GSS系列的都应该很熟悉了

线段树维护的前缀最大子段和，后缀最大子段和，和区间最大子段和

那么我们就可以很容易的写出他合并orpushup

void pushup(node &a,node x,node y) {
	a.ans=max(max(x.ans,y.ans),x.rk+y.lk);
	a.lk=max(x.sum+y.lk,x.lk);
   	a.rk=max(y.sum+x.rk,y.rk);
	a.sum= x.sum +y.sum;
}

这里写成这种形式对下面的跳链比较友好

查询也是比较套路的 返回一个node，如果在mid两边，再次合并，这里就不多说了

树剖跳链

修改操作：

跳链，修改,和平常一样

查询操作：

x到y的路径是一条链子

如果我们把它伸直，捋平咯，那他就是一串数列

那我们就可以一块一块的合并喽

想一下我们是怎么跳的

是从链的两端跳，一直跳到他们相遇

那我们就维护两端的信息,也就是从起点到现在的x的区间和从现在的y到终点的区间

最后再合并起来,就是整个区间的信息喽

不过要注意合并时候的次序和l,r的交换

也许不swap而分类讨论就没这个东西了吧

我们的一条重链是从浅处到深处依次排列

我们跳的时候是从深处到浅出跳(从两端逼近中间)

所以合并就要考虑清楚了

是合并x，y还是合并y，x

文字说起来不太明白，我举个栗子吧

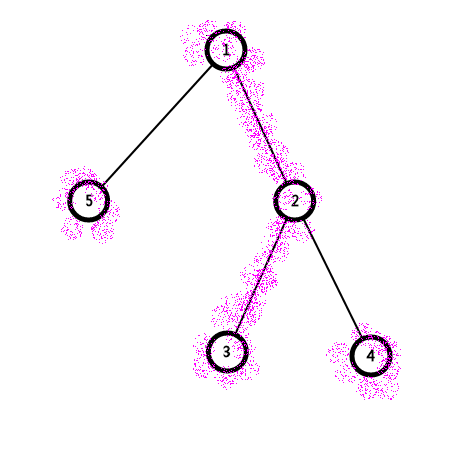
2号权值为-1，其他权值为1，要从4号到5号点

我们先从5号节点跳到1号所属重链

在跳之前我们先查询一下5号的值，得到一个node，和x

合并

我们再从4号节点跳到1号所属重链

在跳之前我们先查询一下4号的值，又得到一个node，和y合并

然后交换x，y(别问我为什么)

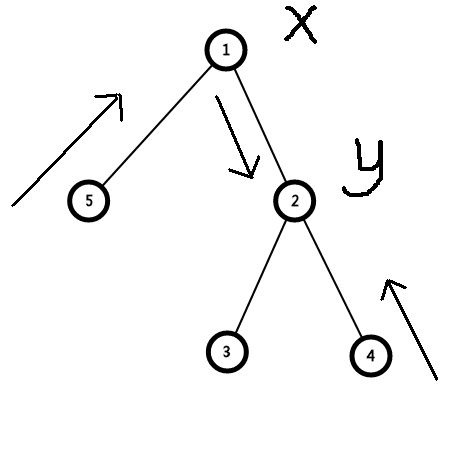
现在x,y都到了一条链子上了（注意前提）

我们考虑一下两端区间的方向

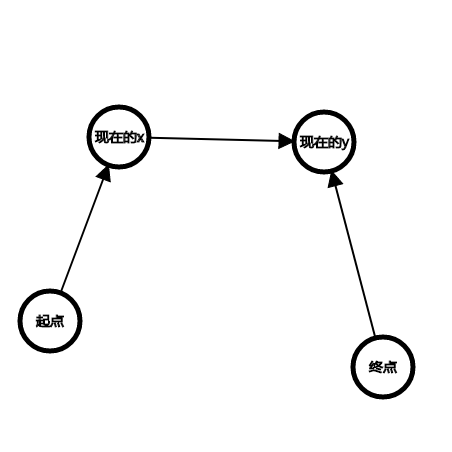
有一个是反着的，我们翻过来其中一个然后全部合并起来就好了

这里给出我的两组简单但易错数据(反正错了我好多次)

5
-1 1 1 1 1
1 5
1 2
2 3
2 4
1
1 4 5
ans=2

5
-3 -2 -1 -2 -3
1 2
2 3
1 4
4 5
2
2 3 4 2
1 2 5
ans=6

代码

#include <bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<=b;++i)
using namespace std;
const int N=6e5+7;
const int inf=0x3f3f3f3f;
inline int read() {
	int x=0,f=1;char s=getchar();
	for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
	for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
	return x*f;
}
vector<int> G[N];
int n,m;
int a[N],w[N],idx[N],top[N],son[N],siz[N],f[N],dep[N],cnt;
inline int max(const int &x,const int &y) {return x>y?x:y;}
void dfs1(int u,int fa) {
	f[u]=fa;
	siz[u]=1;
	dep[u]=dep[fa]+1;
	for(std::vector<int>::iterator it=G[u].begin();it!=G[u].end();++it) {
		if(fa==*it) continue;
		dfs1(*it,u);
		siz[u]+=siz[*it];
		if(siz[son[u]]<siz[*it]) son[u]=*it;
	}
}
void dfs2(int u,int topf) {
	idx[u]=++cnt;
	a[cnt]=w[u];
	top[u]=topf;
	if(!son[u]) return;
	dfs2(son[u],topf);
	for(std::vector<int>::iterator it=G[u].begin();it!=G[u].end();++it)
		if(!idx[*it]) dfs2(*it,*it);
}
namespace seg_tree {
	#define ls rt<<1
	#define rs rt<<1|1
	struct node {
		int l,r,siz,lk,rk,ans,lazy,sum;
	}e[N<<2];
	inline void pushup(node &a,node x,node y) {
		a.ans=max(max(x.ans,y.ans),x.rk+y.lk);
		a.lk=max(x.sum+y.lk,x.lk);
    	a.rk=max(y.sum+x.rk,y.rk);
    	a.sum= x.sum +y.sum;
	}
	void build(int l,int r,int rt) {
		e[rt].l=l,e[rt].r=r,e[rt].siz=r-l+1;
		e[rt].lazy=inf;
		if(l==r) {
			e[rt].sum=a[l];
			e[rt].lk=e[rt].rk=e[rt].ans=max(a[l],0);
			return;
		}
		int mid=(l+r)>>1;
		build(l,mid,ls);
		build(mid+1,r,rs);
		pushup(e[rt],e[ls],e[rs]);
	}
	inline void tag(int rt,int k) {
		e[rt].sum=e[rt].siz*k;
		if(k>=0) e[rt].lk=e[rt].rk=e[rt].ans=e[rt].sum;
		else e[rt].lk=e[rt].rk=e[rt].ans=0;
		e[rt].lazy=k;
	}
	inline void pushdown(int rt) {
		if(e[rt].lazy!=inf) {
			tag(ls,e[rt].lazy);
			tag(rs,e[rt].lazy);
			e[rt].lazy=inf;
		}
	}
	void modify(int L,int R,int k,int rt) {
		if(L<=e[rt].l&&e[rt].r<=R) {
			tag(rt,k);
			return;
		}
		pushdown(rt);
		int mid=(e[rt].l+e[rt].r)>>1;
		if(L<=mid) modify(L,R,k,ls);
		if(R>mid) modify(L,R,k,rs);
		pushup(e[rt],e[ls],e[rs]);
	}
	node query(int L,int R,int rt) {
		if(L<=e[rt].l&&e[rt].r<=R) return e[rt];
		pushdown(rt);
		int mid=(e[rt].l+e[rt].r)>>1;
		if(L<=mid && R>mid) {
			node a=query(L,R,ls),b=query(L,R,rs),c;
			pushup(c,a,b);
			return c;
		}
		if(L<=mid) return query(L,R,ls);
		if(R>mid) return query(L,R,rs);
	}
}
void QQ(int x,int y) {
	seg_tree::node tot_x={},tot_y={};
	while(top[x]!=top[y]) {
		if(dep[top[x]]<dep[top[y]]) swap(x,y),swap(tot_x,tot_y);
		seg_tree::node tmp=seg_tree::query(idx[top[x]],idx[x],1);
		seg_tree::pushup(tot_x,tmp,tot_x);
		x=f[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y),swap(tot_x,tot_y);
	seg_tree::node tmp=seg_tree::query(idx[x],idx[y],1);
	swap(tot_x.lk,tot_x.rk);
	seg_tree::pushup(tot_x,tot_x,tmp);
	seg_tree::pushup(tot_y,tot_x,tot_y);
	printf("%d\n",tot_y.ans);
}
void CC(int x,int y,int c) {
	while(top[x]!=top[y]) {
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		seg_tree::modify(idx[top[x]],idx[x],c,1);
		x=f[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	seg_tree::modify(idx[x],idx[y],c,1);
}
int main() {
	n=read();
	FOR(i,1,n) w[i]=read();
	FOR(i,2,n) {
		int x=read(),y=read();
		G[x].push_back(y);
		G[y].push_back(x);
	}
	dfs1(1,0);
	dfs2(1,1);
	seg_tree::build(1,n,1);
	m=read();
	FOR(i,1,m) {
		int opt=read(),x=read(),y=read(),z;
		if(opt==1) QQ(x,y);
		else z=read(),CC(x,y,z);
	}
	return 0;
}