关于svm

svm的研究一下，越研究越发现深入。下面谈一些我个人一些拙见。

svm计算基础是逻辑回归（logistic regression），其实一切二元分类的鼻祖我觉得都是logistic regress。

公式如下：

那么当我们谋求一个超平面（在二维里面超"线"）y = w.T * x + b来实现分类，其实就是g（w.T *x + b），注意这里有点反人类，在前者y是因变量，但是在g(z)中，y变成了自变量，是一个层级关系；后者意义就是我作为一个函数，函数的意义满足某个计算规则的点，扔到里面去，可以用于做分类；从下图可以看到，下面的三条线（超平面），都符合函数w.T + b的模式，但是扔到g(z)里面的结果预期是不一样，相当于将g(1）和g（-1），g（0）（注意这里的-1和1都是极值，为了保证最大间隔的极值，其实y是连续的，可以取任意实数）；那么就是可以实现基于sigmoid函数的分类。当然g的取值也是二元的-1，和+1。

那么下面就是重点讨论w.T*x + b这个超平面。在讨论这个公式之前，我们首先确定一下概念，有了上图之后，可以简单的解释一下这个问题，所谓的支持向量机，就是实现查找到实现可分间隔最大化的边缘平面的算法；那么支持向量就是分布在变换平面上面的点，之所以称之为支持向量就是因为他么支撑了边缘平面，那么支持向量后面的那些点都不需要关心了，他们的位置对于分类没有任何帮助，所以就属于非支撑（骨干）的点。到此简单讲解了一下支持向量机的概念。

那么如何来搞掂这个最大化边缘平面呢？我在刚开始接触的时候其实并不是特别理解最大化间距，但是看到上图之后，其实你会发现如果不断的旋转移动这三条线，你会发现为了实现分类，三条线的相对位置其实是在不断变化的，svm的算法的目的就是实现让分类边缘线1）平行，2）间隔最大；那么为什么要最大呢？这样分类倾向性会更加明显一些，一些个似是而非的点可能性将会非常小；极端情况，在逻辑回归的场景下，就是一条线，如果点在这条线上面了，你说怎么分？所以svm通过"宽带"这种分割模式，在很大程度上加强的分类的倾向性。

关于最大化边缘平面距离就是最大化间隔问题，那么间隔，就要提到两种间隔，分别是函数间隔和几何间隔，函数间隔：

点x到超平面的间隔，或者说距离就是w.T *x + b，但是因为分类，所以距离有正负，为了获知分类正确性，前面乘以y，y就是分类，只有-1和1两个值，之所以这样处理，如果分类正确，说明y和f(x)的符号一致，距离必然正值，反之负值，所以通过符号就可以判断来准确性。我们让边缘平面的y值取-1和1，所以在边缘超平面的点一定是=1或者=-1，那么y的取值范围是大于1，小于-1的；通过函数间隔，其实我们目标是求出这些点到超平面的距离的最小值：

这样人为的定义的距离有一个问题，就是如果等比例放大w和b，将会导致距离也变化，但是我们知道等比例改变w和b将会导致距离变化（对应的y值也等比例增加），但是此时超平面并没有变化，但是距离却不再和之前相等；所以此时引入了几何距离：

下面的是推导过程，可以得出几何距离。

处于同样的理由，我们让y*r，这个就是最终的几何距离公式：

这样我们求解最大间隔问题，其实就是求：

约束条件（s.t）为

这样，我们其实设r^值为1，并不影响优化效果，来简化处理公式（为什么改成1可以？）：

那么如何求解呢？

这里有一个非常美妙的变化，就是上面的公式可以变型为min函数：

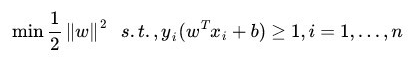
更加精妙的变形在于通过下式将约束和min函数包容起来了：

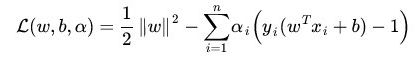
其实为什么可以把约束和主题函数放在一起？看下面的公式：

ai是大于0的，yi（w.T*xi+b)一定是>=1，因为为了实现L(w,b,a)的最大化，一定是||w||**2/2的后面部分一定是等于0，才能够实现最大化，所谓约束，拉格朗日对偶的公式里面已经成为了一种前置假设。这个是我之前的理解，但是这里其实牵涉到凸优化的问题，并不是简单的极值。比如下面的变形，其实使用的凸优化的知识：

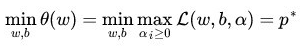
然后进行max和min位置交换：

这种等价交换是有条件的（正常情况下d*<=p*），这种转换使得计算变得简单，但是，为什么变得简单了，为什么先min后max就会简化运算？不懂。

数学最优化模型是下图所示，f(x)是要求最小化的函数，hj是等式约束，gk是不等式约束。

有了有了优化模型的描述，我们再来看看min-max等价交换的KKT条件：

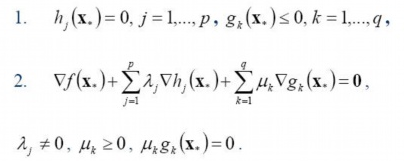
求对偶问题三个步骤：

1）对w和b求对偶：

带入到上面L(w,b,a)公式中，可得：

最后经过推到：

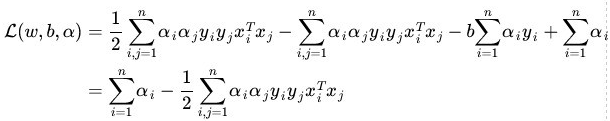
这里注意，早期全部都是i但是到了推倒的最后几步出现了i，j的分割：

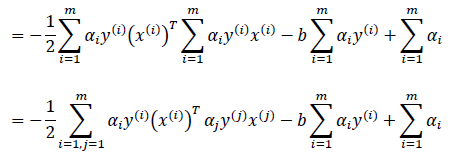
这里的其实是一个两层循环，外层循环是i，里层循环是j；这个两层循环的累加完成了矩阵间的乘法运算。

第二步，根据上一步推导出来的公式进行求a值；

有了a之后，根据偏导数求出的公式可以解出w，然后通过下面的公式可以求出b，从公式上面来看应该是f(x)的最大值和最小值的均值，但是为什么是这个求b值呢？

 

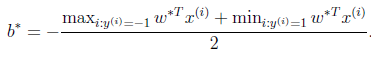
第三步，即最后一步，通过SMO算法求解a；但是到这里我懵逼了，在第二步的时候，不是已经把a值给求出来了吗，怎么又求了一遍？

核函数

其实数据大多数场景都是线性不可分的，就是无法采用一条直线进行分类，需要曲线，曲线就是多项式，计算比较复杂，这个时候，如果是升维，那么很多时候可以简化问题，这个时候，核函数就出现了。

在讲核函数之前，我们先看一个前置知识：向量内积。

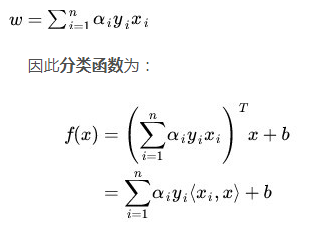
通过上面公式，可以很清晰的看到转置被处理成了内积，OK，核函数的本质其实就是把低维数据映射高维数据，怎么映射？

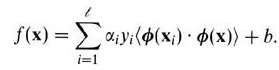
简单讲就是将原来x->φ(x)，那么核函数的高明之处在于他的计算并不是在映射到高维之后，再计算，如果那样的话，求解可能会有"维度灾难"。比如：

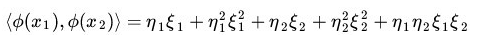
这是一个五维空间，计算量比较大了，但是核函数不是对于分解之后在计算，而是找到了一种等价的形式：

来对其进行计算，这样的话，你会发现计算简单很多。而且核函数的形式和咱么上面提到公式中内积的形式是一致的（注意，核函数可并不是为了svm的内积而生的，而是有气自己数学应用场景的）。所以，你可以指定一些核函数来进行提升维度处理，同时还避免了高维的海量特征的计算。

常用的核函数包括：

1. 多项式；上面举例(<x1,x2> + 1)**2就是一个多项式核函数的例子；

2. 高斯核函数，这个可能是应用最广泛的一种和函数了。

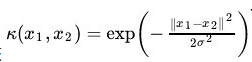
3. 线性核函数，这个主要就是用于兼容，当不需要提高维度，但是为了计算的统一性，采用这个核函数可以保证计算逻辑的一致性。

 

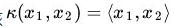
关于松弛变量

svm中对于离群点有专门的处理，所谓离群点是指下图中的蓝色部分。所谓离群点是指貌似对方，但是其实是自己人那些点，但是因为位置比较尴尬，所以svm设置了一个松弛变量，就是允许在一定范围内的离群点，这样可以这样讲，其实允许在"宽带"之间有一些点，这些点将会基于到宽带两边的距离来进行划分。避免宽带间点无法被处理。

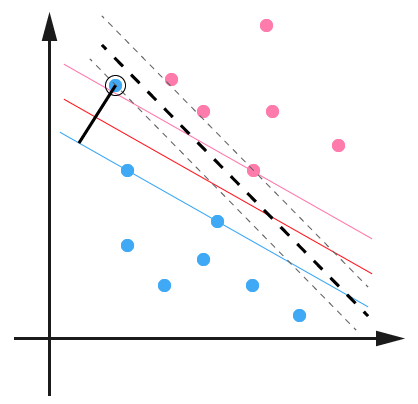
我们继续拿函数距离来做表达（为什么这里又采用了函数距离，而不是集合距离），此时距离赢不再是1，而是减去一个变量。

ξi不可以任意大的，于是添加了一个C作为限制

于是我们有了新的L(w,b,a)：

后面处理的流程和上面很类似，首先是求导获取极值取值：

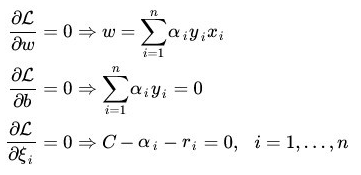
带入到拉格朗日的公式中，可以求得：

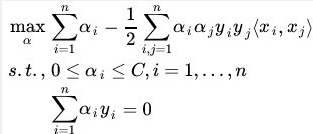
结果函数和之前是一样的，但是增加了一项约束：ai<=C（因为C-ai-ri=0，所以C必然大于等于ai）

最后是SMO算法，其实smo算法才是向量机的核心，他解决了如何求解a的关键，但是讲真，我看的资料并没有把smo算法讲明白。下一轮再研究吧。

 

参考

https://blog.csdn.net/v_JULY_v/article/details/7624837