NOIP初赛知识点

http://www.doc88.com/p-9982181637642.html

连载中……

（一）八大排序算法

下面这张表摘自博客http://blog.csdn.net/whuslei/article/details/6442755/

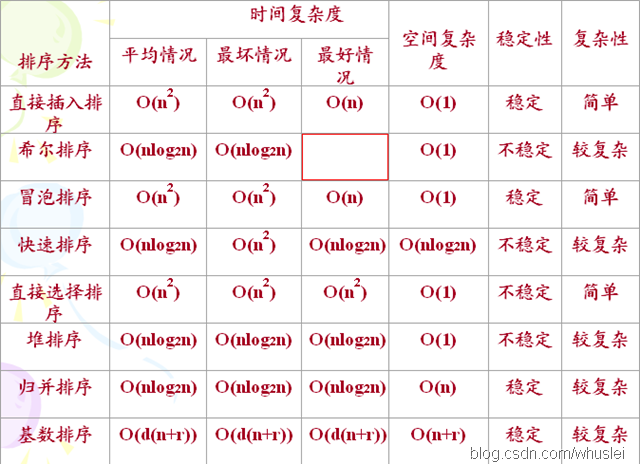
排序算法基本就考这张表

另1：快排找第k大的数，O(N)

另2：拓扑排序。

拓扑排序对象：有向无环图

拓扑排序方法：

1、首先选出一个入度为0的点

2、将改点输出，然后删除所有与该点相连的边

3、重复步骤1、2，直到输出了n个点

对于上面的那个图，答案是：

通常，一个有向无环图可以有一个或多个拓扑排序序列。

另3：计数排序

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算。当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）

计数排序是稳定的

（二）进制转换

（1）二、四、八、十六互转通用方法：

以八进制转二进制为例

先把关系表列出来：

八进制数	二进制数
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

二转八：

例如：10010011

2^3=8

所以使用三位一合的方法（以小数点为分界）

对照上面的表 10 010 011

2  2  3

八转二：

同理，一位三分法

例如：7643

对照上面的表 7    6    4    3

111  110  100  011

（2） 二转十和十转二

二转十：个位*2^0，十位*2^1，百位*2^2…… 若是小数，十分位*2^-1，百分位*2^-2……然后加起来就行了

十转二：整数转换：短除法，倒取余数

小数转换：整数部分同上，小数部分不断*2，取整数部分，直到乘到1为止

（三）古怪的位运算

与（按位与& 逻辑与∧） 11取1 其它取0

或（按位或| 逻辑或∨） 00取0 其它取1

异或（按位异或^） 一样取0 不一样取1

取反（按位取反~ 逻辑取反﹁或!） 1变0，0变1

优先级：~ > & > ^ > |

位运算：

对于两个数进行按位运算时，先将两个数转化为二进制（小数点对齐），然后将每一位都进行逻辑运算（注意空位补0）

比如，计算21^2

先转换为二进制

21=(10101)2

2=(10)2

然后按位进行逻辑异或运算

10101

^   10

————

10111

最后得出结果(10111)2=23

逻辑运算：

判断逻辑运算式的真假值时，把数带进去算一下就好了

例：A=true，B=false，C=false，D=true时

(A∧B)∨(C∧D)=0

((A∧B)∨C)∧D=0

A∧((B∨C)∨D)=1

(A∧(B∨C))∨D=1

(A∨B)∧(C∨D)=1

遇到这种题细心计算就好了

（四）集合论

集合就是同一种东西组成的一大坨东西

集合的三个性质：

【1】确定性. 一个元素a是否属于一个集合A,是确定的,不存在既属于,又不属于的关系.
【2】互异性. 同一个集合内,任何两个元素均是不同的.
【3】无序性. 同一个集合内,元素是无序的,即｛a,b}与{b,a}是同一个集合.

一些概念：

空集：没用任何元素的集合

子集：若集合A中的所有元素都包含在集合B中，则定义集合A是集合B的子集。符号为A ⊆ B。例如{1,2} 是{1,2,3} 的子集，但{1,4} 就不是{1,2,3} 的子集。依照定义，任一个集合也是本身的子集，不考虑本身的子集称为真子集。

并集：指两个集合所有包含的部分，符号∪。如集合{1,2,3}和集合{2,3,4}的交集为集合{1,2,3,4}。（可以理解为∨）

交集：指两个集合间相同的部分，符号∩。如集合{1,2,3}和集合{2,3,4}的交集为集合{2,3}。（可以理解为∧）

相对差集：指集合A中有但集合B中没有的部分，符号为A \ B，相对差集{1,2,3} \ {2,3,4} 为{1}。注意：这玩意是单向的，即A\B和B\A是不同的。

对称差：指只在集合A及B中的其中一个出现，没有在其交集中出现的元素。符号为A △ B或A⊕B或A——B，例如集合{1,2,3} 和{2,3,4} 的对称差为{1,4}。

如果上面的看不太懂，可以看看下面的图（摘自百度百科）：

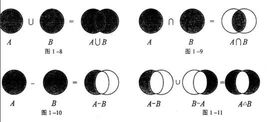
针对这张图：

左上：并集，A ∪ B；

右上：交集，A ∩ B；

左下：A对于B的相对差集，A \ B；

右下：对称差，A △ B或A⊕B或A——B；

来道例题：

设全集I={a,b,c,d,e,f,g}，集合A={a,b,c}，B={b,d,e}，C={e,f,g}，那么集合A{a,b,c,d}B{a,b,d,e}C{b,d,e}合(A—B)∪(~C∩B)为（）。
A.{a,b,c,d}  B.{a,b,d,e}  C.{b,d,e}  D.{b,c,d,e}  E.{d,f,g}

解：A——B为A中的“月牙”，即为ac；~C为abcd，再取和B的并集为bd，然后再取并集abcd。

所以答案为A

注意：注意优先级！！！~优先于∩优先于∪

（五）二叉树

定义：
n个结点的有限集，每个结点至多只有两棵子树，子树也是二叉树。每个结点可以有左孩子和右孩子，顺序不可颠倒。

概念：

度：某个结点孩子的个数
叶子：度为0的结点

深度：二叉树的层数

满二叉树：深度为
n且结点数为2n-1的二叉树

完全二叉树：深度为k，1~k-1层为满二叉树，第k层叶子节点集中在左边的二

n个结点所组成的不同形态的二叉树数目为：C(2n,n)/(n+1)

（六）指针

*是指针，取地址

&是取址符，取地址里的值

int *a; //a是地址中的值

b=&c; //b是地址

（七）基本常识

一个字节（byte）由八个二进制位组成

8bit=1byte

完全图：所有顶点之间两两有一条无向边

通讯标准：

1、模拟

2、GCM

3、WCDMA

4、FDD-LTE

5、华为

（八）数论

n^(-m)=1/(n^m)

（九）表达式

先建树

（十）问题求解

1、要耐心地寻找规律
2、要冷静的分析问题
3、不到万不得已决不轻言放弃
4、不懂就蒙一个！

（十一）阅读程序
1、认真计算
2、耐心分析
3、分析不下去就函数（语句作用）
4、千万记得第一个阅读程序要检查
5、多多练习，熟能生巧
6、列出变量变化表

（十二）程序填空
这种题与编程经验和算法学习的程度有关，拿得一分是一分。

~祝大家NOIP取得好成绩~

（完结撒花）

【鼓掌】【啪啪啪】【鼓掌】