深度优先搜索（DFS）和广度优先搜索（BFS）

深度优先搜索（DFS）

广度优先搜索（BFS）

1、介绍

　　广度优先搜索（BFS）是图的另一种遍历方式，与DFS相对，是以广度优先进行搜索。简言之就是先访问图的顶点，然后广度优先访问其邻接点，然后再依次进行被访问点的邻接点，一层一层访问，直至访问完所有点，遍历结束。

2、无向图的广度优先搜索

　　下面是无向图的广度优先搜索过程：

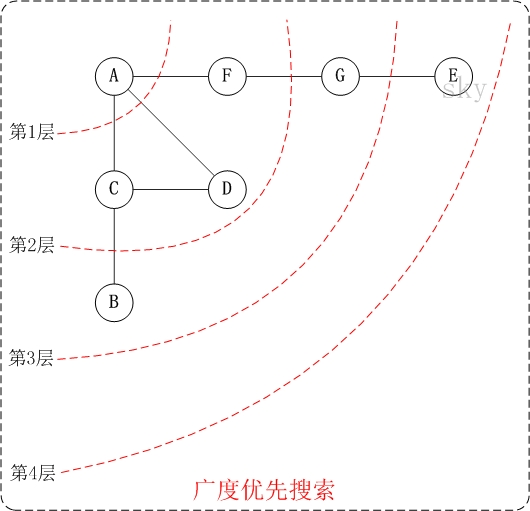
所以遍历结果为：A→C→D→F→B→G→E。

3、有向图的广度优先搜索

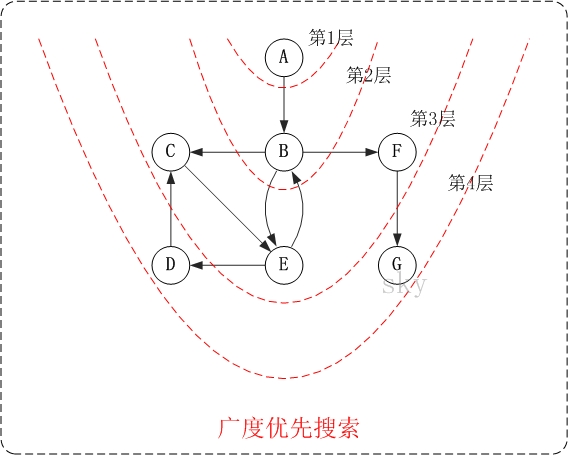
所以遍历结果为：A→B→C→E→F→D→G。

4. C++代码

 #include <iostream>
 #include <queue>
 using namespace std;

 #define MAX 20

 int visited[MAX];
 int map[MAX][MAX];

 void bfs(int start, int n)
 {
     queue<int> q;
     int q_top;
     cout << start << " ";
     visited[start] = ;
     for (int i = ; i <= n; i++)
         if (map[start][i] ==  && visited[i] == )
         {
             q.push(i);
             visited[i] = ;
         }

     while (!q.empty())
     {
         q_top = q.front();
         q.pop();
         cout << q_top << " ";
         for (int i = ; i <= n; i++)
             if (map[q_top][i] ==  && visited[i] == )
             {
                 q.push(i);
                 visited[i] = ;
             }
     }
 }

 int main(int argc, char * argv[])
 {
     int num_vex, num_edge, x, y;
     cout << "Input number of nodes and edges >> ";
     cin >> num_vex >> num_edge;  //num_vex 顶点; num_edges 边数
     for (int i = ; i< MAX; i++)
         for (int j = ; j < MAX; j++)
             map[i][j] = ;

     for (int i = ; i <= num_vex; i++)
         visited[i] = ;

     for (int i = ; i <= num_edge; i++)
     {
         cin >> x >> y;
         map[x][y] = map[y][x] = ;
     }
     bfs(, num_vex);
     return ;
 }

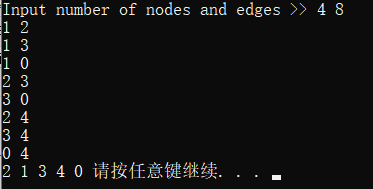
输入输出：

 5. C语言代码

参考资料

1. 深度优先搜索和广度优先搜索