Windows定位窗口对应的exe文件

一、说明

以下两种情况我们会想要定位窗口是由哪个exe文件，或者什么命令启用

第一种是：广告窗口，现在经常时不时冒出一个广告窗口，要么是完全看不出哪个程序启动，要么是虽然大概知道是哪个应用启动（比如wps）但广告经常不是由主exe启动的我们想要具体确定到对应的exe文件。

第二种是：系统功能窗口，比如下边的“Internet选项”我们经常会启动它来修改代理，启动“Internet选项”我们经常是先启动IE再通过IE的工具菜单来启动这显得很麻烦，我们此时就想知道这个窗口对应的exe文件是哪个或者启动命令是什么。

本文就源于自己想确定“Internet选项”窗口对应的启动命令，这里也以此来进行“Windows定位窗口对应exe文件”的演示。

定位需要用到Process Explorer工具，主要参考：http://blog.sina.com.cn/s/blog_a2f8a4890101ktuh.html

二、Process Explorer安装使用

Sysinternals是微软提供的一套windows平台安全测试小工具，更通俗而言可以理解为ps、netstat等系统功能的高级版（功能上的advance，对接近系统内核硬件而言则是low-level）

Process Explorer是Sysinternals套件中的一个小工具，可以认为是高级版的任务管理器，我们可以借助它来定位窗口对应exe文件和启动命令

2.1 下载

Sysinternals套件下载页面：https://docs.microsoft.com/zh-cn/sysinternals/downloads/

开头那个Sysinternals Suite是整个Sysinternals套件包含所有工具，我这里就是直接下载整个套件，也可以单个下载下边的都是单个工具的下载链接

Process Explorer直接下载页面：https://docs.microsoft.com/zh-cn/sysinternals/downloads/process-explorer

2.2 使用

2.2.1 启动

下载后就是一个zip包解压到自己想要的目录即可，然后打开cmd切换到该目录下，使用procexp.exe命令启动

启动后程序界面如下，主要窗口就是和任务管理器类似，显示进程

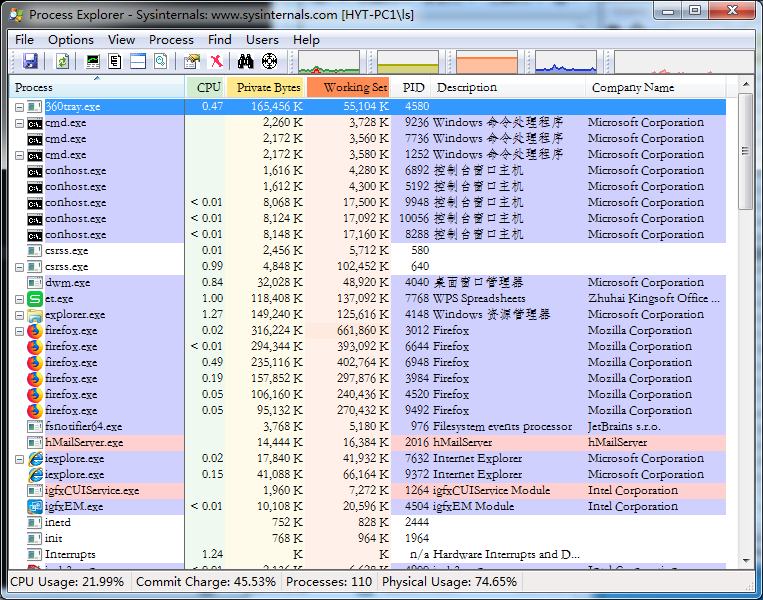
2.2.2 使用chrome等非IE浏览器启动“Internet选项”窗口

IE启动的话，启动命令会显示为IE本身（iexplore.exe），chrome等浏览器启动才能得到我们想要的启动命令（这应该是IE开发时import了dll而chrome等只是启动时去调用dll）

2.2.3 进行定位

鼠标左键按住定位器，按提示托动到“Intenet选项”窗口，再松开

完成后焦点就会给到窗口对应的进程上

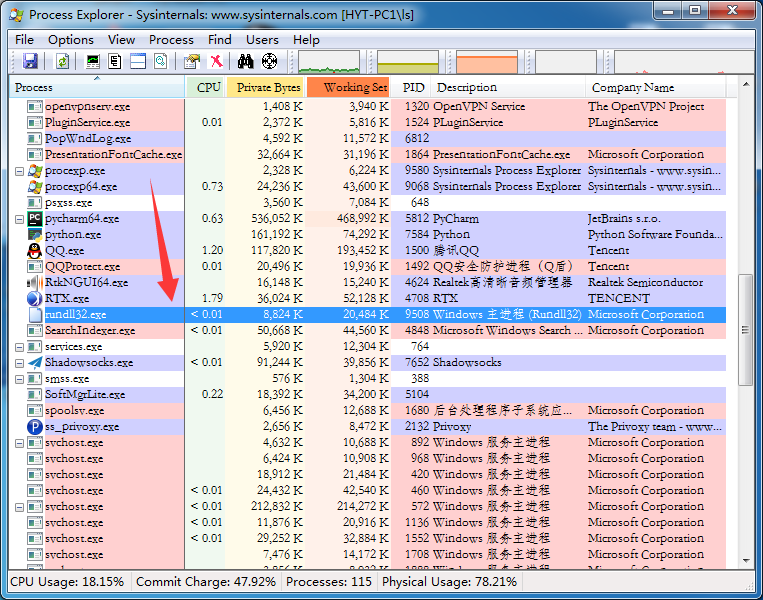
直接在其上双击，或都通过右键唤出菜单选择“Properties”项查看

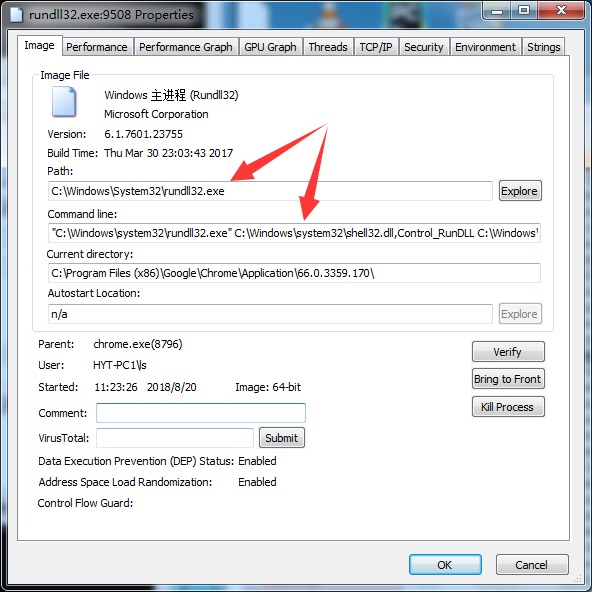
Path就是窗口启动的exe，Command line就是窗口具体的启动命令。

这里“Internet选项”的具体启动命令如下（也就是在cmd窗口使用该命令就可以直接启动“Internet选项了”）：

"C:\Windows\system32\rundll32.exe" C:\Windows\system32\shell32.dll,Control_RunDLL C:\Windows\system32\inetcpl.cpl,,

参考：

http://blog.sina.com.cn/s/blog_a2f8a4890101ktuh.html