Java实现 洛谷 P1280 尼克的任务

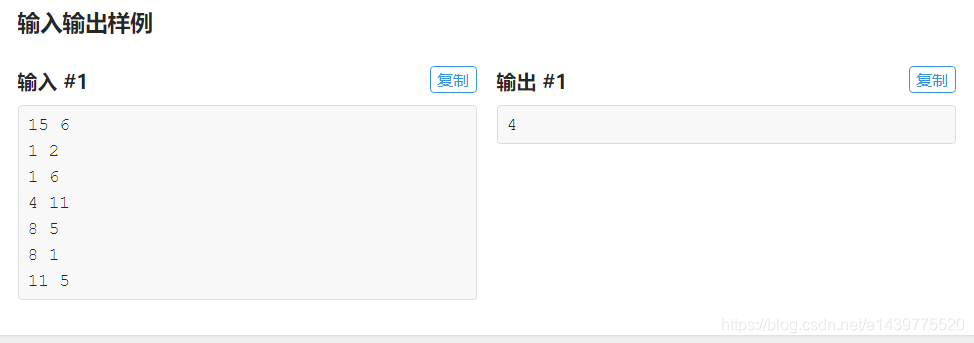
import java.util.Scanner;

public class Main {
	public static class edg{
		private int to;
		private int next;

		public edg() {

		}
		public edg(int to,int next) {
			this.next=next;
			this.to=to;
		}
	}

	static int head[],t=0;
	static edg a[];
      public static void main(String[] args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int m=sc.nextInt();
		a=new edg[n*5];
		head=new int[n*5];
		for (int i = 0; i<n*5; i++) {
			head[i]=-1;
		}
		for (int i = 0; i <m; i++) {
			int x=sc.nextInt();
			int y=sc.nextInt();
			add(x,y);
		}
		int f[]=new int[n+2];
		for (int i =n; i>0; i--) {
			if(head[i]==-1) {
				f[i]+=f[i+1]+1;
			}else {
				for (int j =head[i]; j!=-1; j=a[j].next) {
					int k=a[j].to;
					if(i+k<=n) {
						f[i]=Math.max(f[i],f[i+k]);
					}
				}
			}
		}
		System.out.println(f[1]);

	}
      public static void add(int x,int y) {
    	  a[t]=new edg(y,head[x]);
    	  head[x]=t++;

      }
}