题目分享G 二代目

题意：有n组数，每组包含两个数，问在每组只能取一个的前提下能组成的最长的从1开始的连续自然数有几个？

分析：刚学了差分约束系统，很容易往转换成图的方向去想

将他读入的这n组数当成边读入

很容易会得到一个图，这个图不一定是连通的，

我们暂时先把他所有极大连通子图划分为两种：一种是 属于树的，另一种是 不属于树的

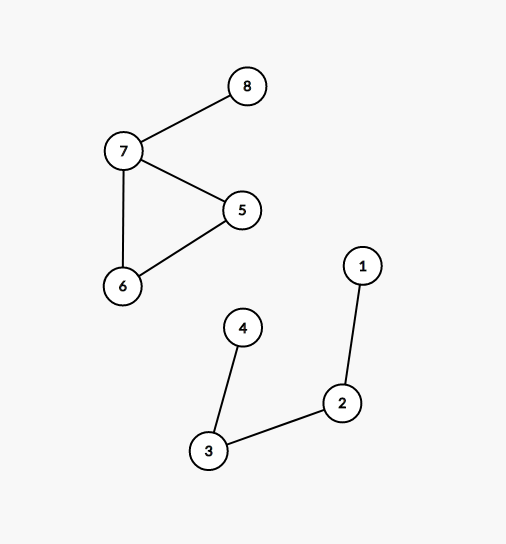
显然，1234是属于树的，而5678则不属于树

对于树来说，显然n个节点的树只能选出n-1个节点来，

这个是很容易证明的，如果我们把不选的那个节点作为根节点，那么显然其他的节点是都可以选的，每个节点只需要用其连向父亲的边即可

再考虑图，其实我们依然可以将每个环缩成点，然后继续考虑缩完点之后剩下的树

首先，对于一颗树来说刚刚已经证明了根节点不选，别的节点都选是最优的

而对于一个环来说一定所有节点都是可以选的，这是显然的

那么如果我将这个环缩成的点作为根，虽然这个环没法在树中被选

但这个环中的每个元素都是被选的

也就是说，只要这个极大连通子图不是树就一定所有节点都能选

而对于树来说，会有一个节点是不能选的，那肯定是让最大的不选是最优的

所以只需要用并查集判断是否是树，如果是树再记录一下最大值即可

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn=1e4+;

int fa[maxn];
int mxp[maxn];

int find(int x)
{
    while(x!=fa[x]) x=fa[x];
    return x;
}

int ya(int x)
{
    int fax=find(x),nowfa;
    while(x!=fax)
    {
        nowfa=fa[x];
        fa[x]=fax;
        x=nowfa;
    }
    return fax;
}

void bing(int x,int y)
{
    int fax=ya(x),fay=ya(y);
    if(fax==fay) mxp[fax]=maxn;
    else fa[fay]=fax,mxp[fax]=max(mxp[fax],mxp[fay]);
}

int main()
{
    int n,x,y;
    for(int i=;i<maxn;i++) fa[i]=mxp[i]=i;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d",&x,&y);
        bing(x,y);
    }
    int ans=maxn;
    for(int i=;i<maxn;i++) ya(i);
    for(int i=;i<maxn;i++) ans=min(ans,mxp[fa[i]]);
    printf("%d",ans-);
    return ;
}