K-Means & Sequential Leader Clustering

2017-12-31 19:08:37

k-平均算法源于信号处理中的一种向量量化方法，现在则更多地作为一种聚类分析方法流行于数据挖掘领域。k-means的目的是：把样本划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准。

这个问题在计算上是困难的（NP困难），不过存在高效的启发式算法。一般情况下，都使用效率比较高的启发式算法，它们能够快速收敛于一个局部最优解。这些算法通常类似于通过迭代优化方法处理高斯混合分布的最大期望算法（EM算法）。

K-means比较适合数据类型是球状的数据，也就是不同的簇的形状是一球一球的。

一、簇评估

聚类问题由于是无监督的问题，可以说是没有什么标准答案的，也就是说怎么分类都是可能的。

另外坐标的变换也是会影响最终的结果的：

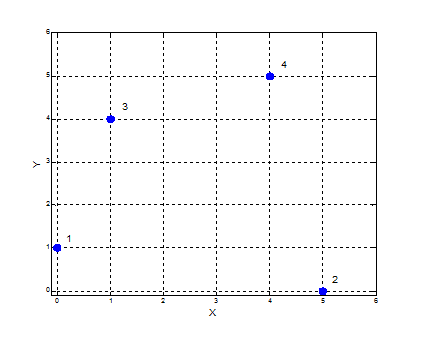
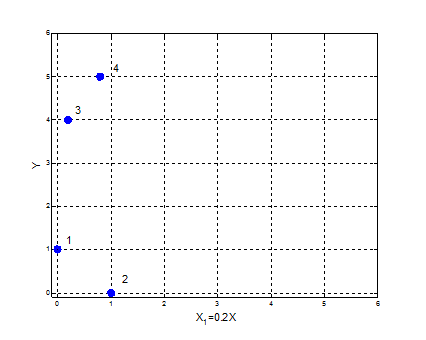
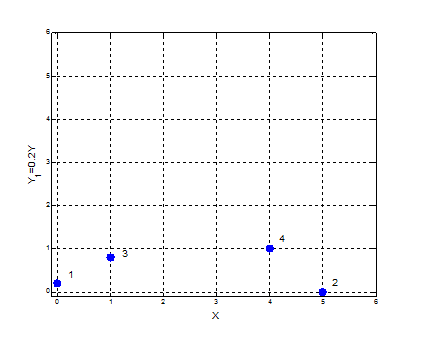
那么该如何对聚类的结果进行评判呢？

• 计算类似聚合度的概念

也就是通过计算每个数据和他到其类均值的距离平方，最后再求和得到最后的数值，显然，数值越低表征聚类效果越好。同样的，这种判断方法也是针对一团一团的数据比较好用。

• Silhouette

对每个数据点计算s（i）的值，其中b（i）表示其到数据点i到各个其他类的距离的均值的最小值，a（i）则表示数据点i到自身这个类的距离的均值。

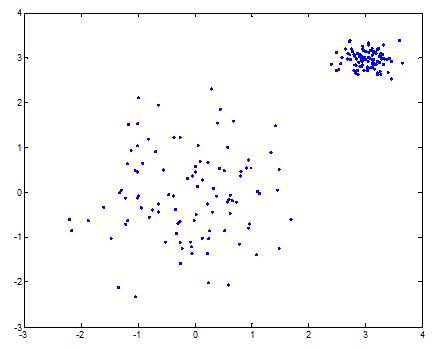
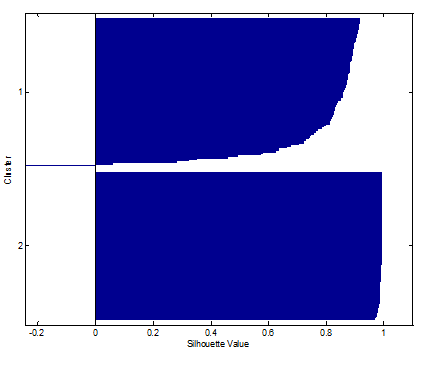
对于聚合程度高的类他的S图是比较规整的，对于分散的则是比较参差不齐的。

二、K-Means算法

K-Means顾名思义就是k个均值的意思，K-Means算法本质上也是一种EM算法思想的应用。

该算法非常形象的表述了如何计算收敛到k个类的一个过程：

首先生成k个类（也就是随机生成k个中心）；

然后通过k个均值，得到属于他们的数据点；

通过得到的中心点重新计算其k个均值；

loop第二步，第三步直到k个均值保持不变。

因为k-means比较简单，所以得到了非常广泛的使用，其有如下的优点和缺点。

优点：

1. 收敛迅速，简单高效，适用于一团一团的数据；
2. 算法复杂度O（tkn），t是迭代次数，k类的个数，n数据点的个数；

缺点：

1. k值的选择，初始点的选择都会产生迥异的结果；
2. 对噪点敏感，因为使用的是均值；
3. 对奇怪的形状适用性较差；

三、Sequential Leader Clustering

Sequential Leader Clustering可以处理流数据。K-Means如果看成是把一群人聚集到教室再进行分类的话，那Sequential Leader Clustering就是对每一个进来的同学进行一个分类，所以Sequential Leader Clustering不需要迭代运算，只需要遍历一遍数据集就可以了，值得一提的是这种算法不需要设定k值。

Sequential Leader Clustering需要手动设置一个阈值。

算法流程：

n {\displaystyle n} 个点（可以是样本的一次观察或一个实例）划分到k个聚类中，使得每个点都属于离他最近的均值（此即聚类中心）对应的聚类，以之作为聚类的标准。