Python 零基础 快速入门 趣味教程 (咪博士 海龟绘图 turtle) 1. 神秘朋友

Python (Windows 下) 自带了一个非常有趣的 海龟绘图程序 (turtle)，它是本系列课程的主角。

在 PyCharm 中，新建一个项目，然后在代码编辑器中输入

 import turtle
 turtle.shape("turtle")
 turtle.exitonclick()

运行这段代码，便可以召唤出这位可爱的小精灵

上面的代码中  import turtle  用于导入模块，导入之后就可以应用模块的各种功能了

turtle.shape("turtle") 调用 turtle 的 shape 方法，用于改变海龟的显示方式（默认显示的是一个三角形的小箭头）。执行这句代码之后，turtle 显示为一只形象的小海龟。

turtle.exitonclick() 最后这句是告诉海龟保持住，直到遇到鼠标点击的时候才退出 (exit on click)。不然程序执行得太快，我们还来不及看到海龟，它就已经执行完毕并退出了。

【提示】

• 请不要直接复制、粘贴代码，而是要对照着代码，自己在代码编辑器中一点一点地输入
• Python 是大小写敏感的编程语言，输入代码时，请务必细心，注意字母大小写
• Python 相比其他高级编程语言的一个特别之处，在于强制使用缩进，请不要在每行代码的开头随意添加空白字符（空格、Tab 键等）

现在小海龟位于窗体的正中央，龟头指向右边的方向。

接下来，我们尝试让海龟走两步。

关闭窗口（或点击窗体任何位置自动退出），将编辑器中的代码，更改为下面的样子

 import turtle
 turtle.shape("turtle")
 turtle.forward(200)
 turtle.exitonclick()

运行代码，

我们看到小海龟从屏幕中心出发，沿着龟头的方向（右边），爬行（前进）了一段距离。

这次的代码，跟最开始的代码并没有太多的不同，只增加了 1 条语句 turtle.forward(200) 它的意思就是让海龟沿着当前龟头的指向，前进 200 个单位的距离。

刚才我们已经学会了如何让海龟爬行，接着我们再来看如何让海龟转身。

关闭窗口，将代码改成下面的样子，

 import turtle
 turtle.shape("turtle")
 turtle.left(45)
 turtle.forward(200)
 turtle.exitonclick()

运行之后，将显示下面的效果

这一次，在海龟出发之前（位于窗体正中央，龟头向右），我们先通过 turtle.left(45) 让海龟向左（逆时针）旋转 45 度。此时，海龟仍然位于窗体正中央，但龟头指向屏幕右上方。接着，再让海龟沿着更改后的龟头方向爬行， turtle.forward(200) ，于是就就画出了指向屏幕右上方的一条线段。

【练习】

尝试让小海龟画一个正方形

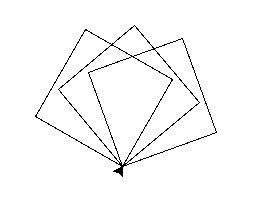
尝试画出 3 个交错叠加的正方形

【原文链接】 http://www.ipaomi.com/2017/11/11/python-零基础-快速入门-趣味教程-咪博士-海龟绘图-turtle-1-神/