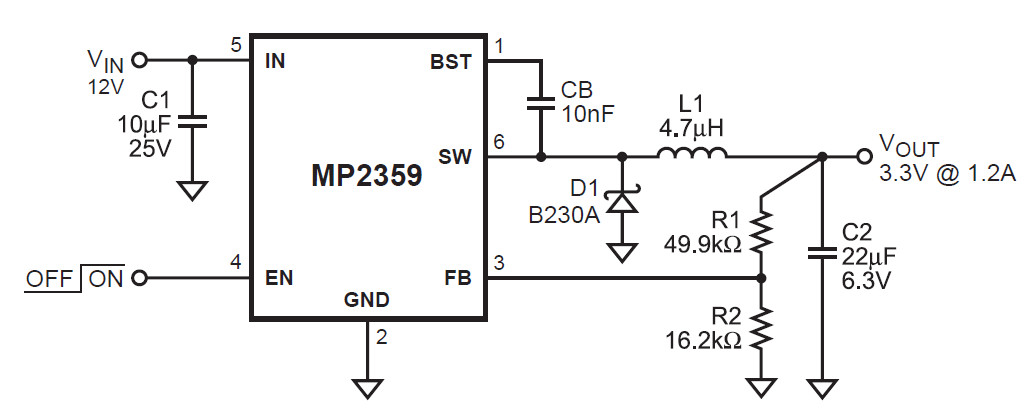
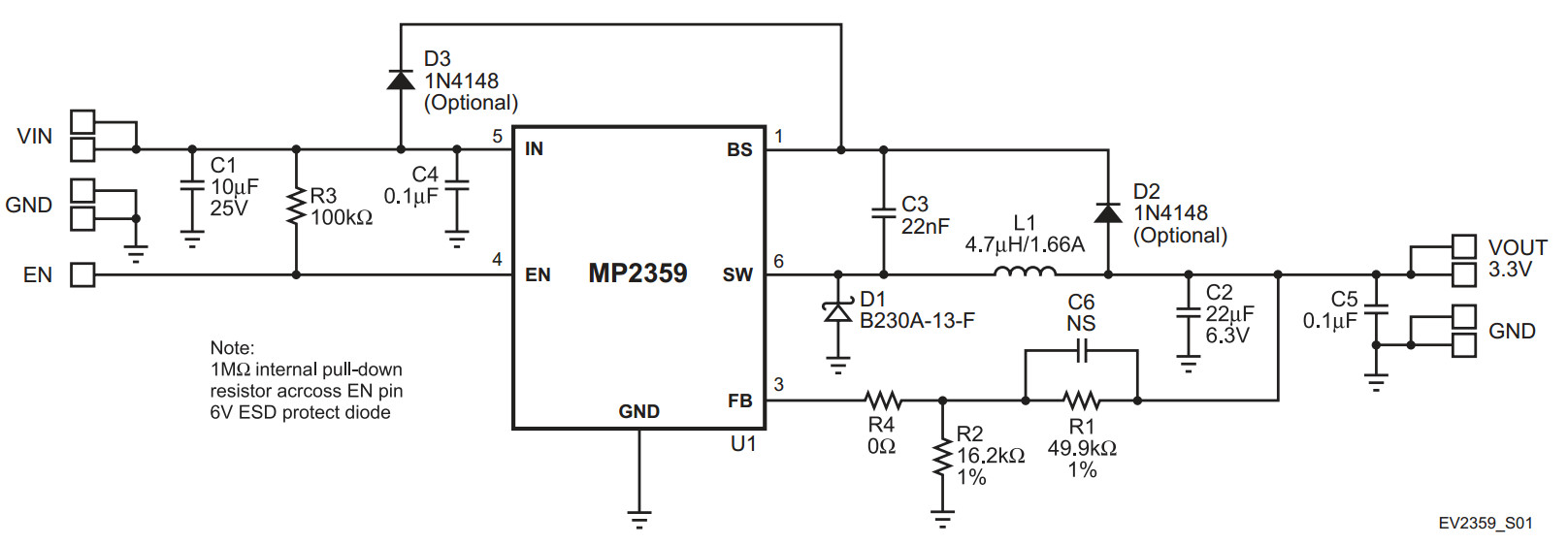
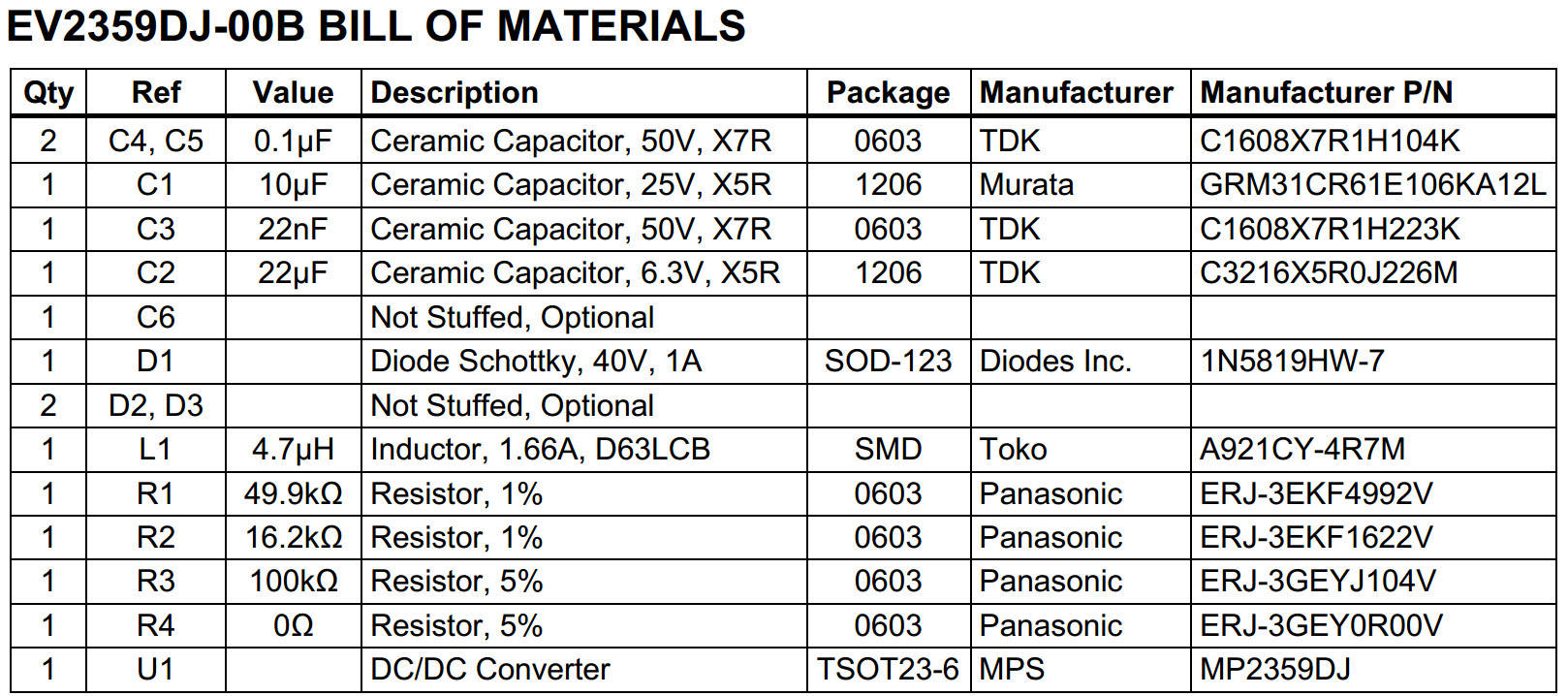
MP2359 1.2A, 24V, 1.4MHz Step-Down Converter in a TSOT23-6
The MP2359 is a monolithic step-down switch mode converter with a built-in power MOSFET.
It achieves 1.2A peak output current over a wide input supply range with excellent load and
line regulation. Current mode operation provides fast transient response and eases loop
stabilization. Fault condition protection includes cycle-by-cycle current limiting and thermal
shutdown. The MP2359 requires a minimum number of readily available standard external
components. The MP2359 is available in TSOT23-6 and SOT23-6 packages.
FEATURES
• 1.2A Peak Output Current
• 0.35Ω Internal Power MOSFET Switch
• Stable with Low ESR Output Ceramic
Capacitors
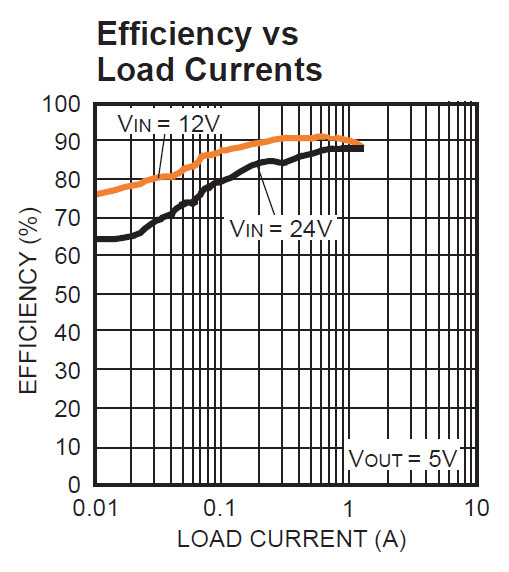
• Up to 92% Efficiency
• 0.1μA Shutdown Mode
• Fixed 1.4MHz Frequency
• Thermal Shutdown
• Cycle-by-Cycle Over Current Protection
• Wide 4.5V to 24V Operating Input Range
• Output Adjustable from 0.81V to 15V
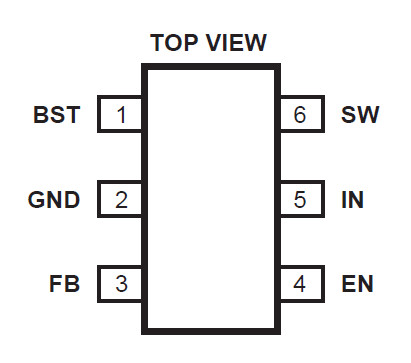
• Available in TSOT23-6 and SOT23-6
Packages
APPLICATIONS
• Distributed Power Systems
• Battery Charger
• Pre-Regulator for Linear Regulators
• WLED Drivers
Recommended Operating Conditions (3)
Supply Voltage VIN ...........................4.5V to 24V
Output Voltage VOUT.......................0.81V to 15V
Ambient Temperature ................ -40°C to +85°C
Max input current into the EN pin............. 300μA
(3) The device function is not guaranteed outside of the recommended operating conditions.

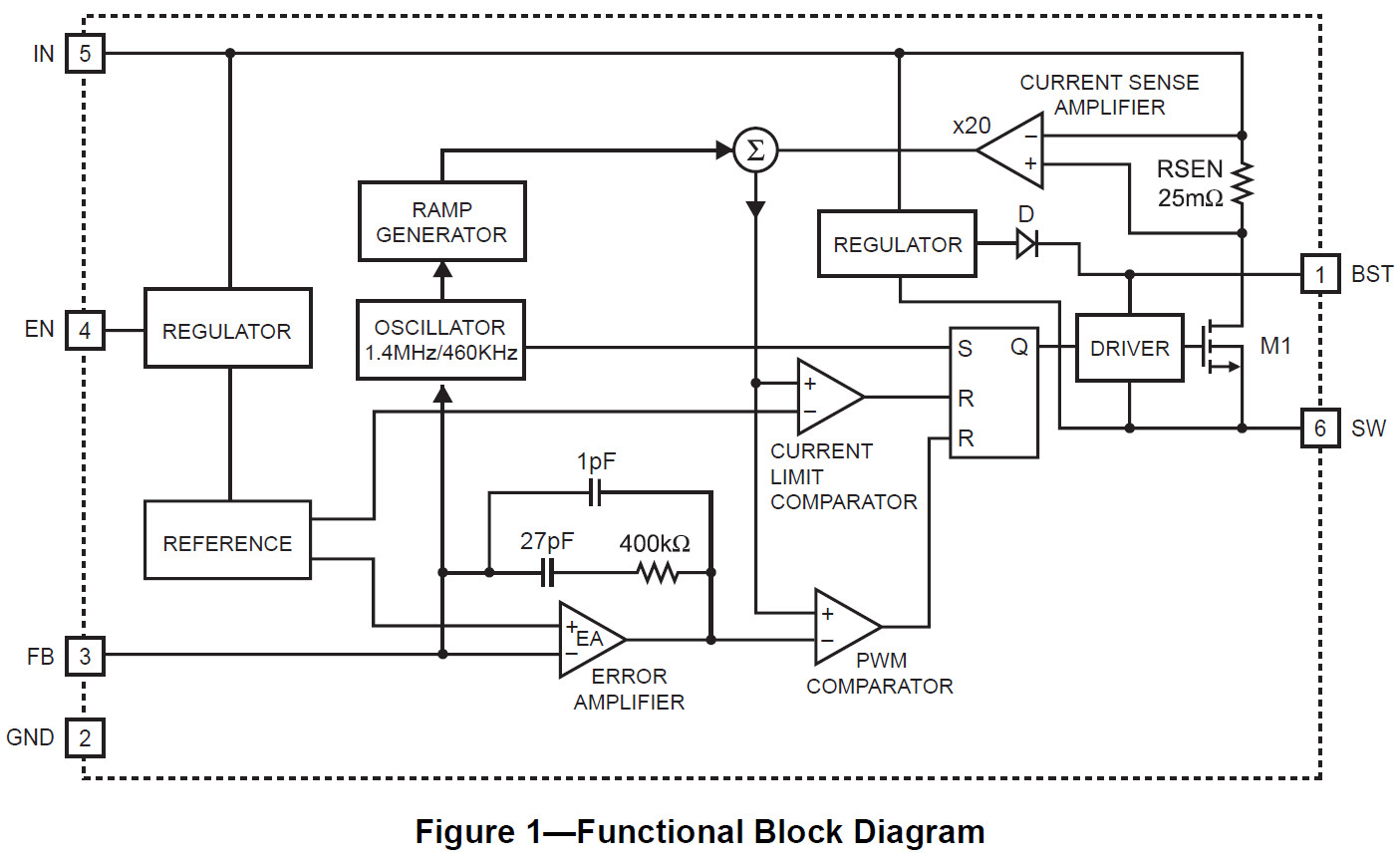

MP2359 1.2A, 24V, 1.4MHz Step-Down Converter in a TSOT23-6的更多相关文章
- 详解ebs接口之客户配置文件导入(二)
------------------------------------ -- 1a. Setup the Org_id ------------------------------------ ex ...
- 嵌入式电路中的BUCK VS LDO【转】
本文转载自:http://blog.chinaunix.net/uid-25906157-id-4125916.html 作为一名FAE,才知硬件知识的匮乏.慢慢积累一点儿硬件知识吧!BUCK和LDO ...
- MySQL: Building the best INDEX for a given SELECT
Table of Contents The ProblemAlgorithmDigressionFirst, some examplesAlgorithm, Step 1 (WHERE "c ...
- Boost Converter
Single Inductor Buck-Boost Converter in Tiny WCSP The TPS63036 is a non inverting buck-boost convert ...
- 具体解释ebs接口之客户配置文件导入(二)
------------------------------------ -- 1a. Setup the Org_id ------------------------------------ ex ...
- WPF converter
单值转换器 将单一值转换为特定类型的值,以日期转换为例如下: 1.定制DateConverter类,其中当值从绑定源传播给绑定目标时,调用方法Convert. 1 public class DateC ...
- PID DC/DC Converter Controller Using a PICmicro Microcontroller
http://www.microchip.com/stellent/idcplg?IdcService=SS_GET_PAGE&nodeId=1824&appnote=en011794 ...
- WPF Converter 使用复杂参数的方法
Step 1在WPF的C#代码文件中给定义复杂类型的变量,并给其赋值:Sample code: List<User>lsUser=....Setp 2在 C#代码对应的XAML 中将此复杂 ...
- AX5511 Boost Converter
GENERAL DESCRIPTION The AX5511 is a current mode step up converter intended for small, low powera ...
随机推荐
- openjudge-NOI 2.6基本算法之动态规划 专题题解目录
1.1759 最长上升子序列 2.1768 最大子矩阵 3.1775 采药 4.1808 公共子序列 5.1944 吃糖果 6.1996 登山 7.2000 最长公共子上升序列 8.2718 移动路线 ...
- Lynx以纯文本的形式下载网页
Lynx是一款基于命令行的web浏览器 [root@test88 ~]# yum install lynx -y [root@test88 ~]# lynx www.baidu.com 以纯文本的形式 ...
- html 简单学习
通过记事本,依照以下四步来创建您的第一张网页. 步骤一:启动记事本 如何启动记事本: 开始 所有程序 附件 记事本 步骤二:用记事本来编辑 HTML 在记事本 ...
- 手游研发CJ抱大腿指南
文摘要:CJ来了,又是一年一度的游戏圈盛事,随着手游行业的迅速崛起,今年CJ上,手游研发商以及发行商必定成为焦点.由于门槛低.市场热.前景好等因素的影响,国内一下子蹦出一大堆手游研发团队.很幸运(或者 ...
- DNS之XX记录
DNS服务器里有两个比较重要的记录.一个叫SOA记录(起始授权机构) 一个叫NS(Name Server)记录(域名服务器)关于这两个记录,很多文章都有解释,但是很多人还是很糊涂.我现在通俗的解释一下 ...
- 洛谷P1554 梦中的统计 题解
题目传送门 这道题暴力又让我过了...数据真的很水(luogu) 暴力枚举n~m的每个数,再统计一次,交付评测...AC #include<bits/stdc++.h> using nam ...
- ASP.NET Zero--1.如何开始
1.加群 群号:104390185,下载这个文件并解压 用VS2015打开aspnet-zero-1.9.0.1 2.修改配置文件 Web项目web.config连接字符串 <add name= ...
- Intel Code Challenge Final Round (Div. 1 + Div. 2, Combined) G - Xor-matic Number of the Graph 线性基好题
G - Xor-matic Number of the Graph 上一道题的加强版本,对于每个联通块需要按位算贡献. #include<bits/stdc++.h> #define LL ...
- JSP内置对象——application对象和out对象
1.application 对象application用于保存所有应用程序的公有数据.它在服务器启动时自动创建,在服务器停止时销毁. 当application对象没有被销毁时,所有用户都可以共享该ap ...
- vue-router在IE11中页面不跳转
情景: IE11浏览器中,在进行正常页面跳转操作后(页面A跳转到页面B),点击浏览器的左上角的‘后退’按钮,点击后,可以看到url地址已经发生了变化(url由页面B变为页面A),hash值也已经是上一 ...
