Linux IO漫谈

本文为原创，转载请注明：http://www.cnblogs.com/gistao/

Background

IO可能是我们接触最频繁的系统调用，比如printf到终端，send content到对端，而今天要讨论的仅是Linux平台下访问本机存储设备相关的IO。如果你对IO相关api的优缺点门清，可以忽略这个随笔啦。

read

read的过程大致如下：

1. 用户malloc出一块内存，然后陷入内核。
2. 内核从磁盘读取内容拷贝到cache。
3. 内核将内容拷贝到用户内存。

缺点比较明显，需要两次拷贝，拷贝是非常耗cpu的。

O_DIRECT

open函数的参数里有这样一个flag，意思是说不需要内核做cache了，内核直接把数据memcpy给用户就好了，这样的优点是可以减少memcpy。但缺点也很明显，没有cache了。

pread

多线程代码并发的访问同一文件是常见的，示例代码如下：

pthread_mutex_lock (mutex);

lseek (SEEK_SET＋1024);
read (buf);

pthread_mutex_unlock (mutex);

这里锁的意义是防治文件指针被其他线程seek走，导致本次read错乱，如何避免掉这个锁呢，就是pread，此函数和read的功能一样，但增加了一个要读取的offset参数，这样就不需要我们显示的加锁了，也许你会联想到strtok和strtok_r。代码改动如下：

pread (fd, buf, offset);

readahead

有时又会遇到下边代码的场景

while (n < max) {
  read (buf[i]);
  on_handle (buf[i]);
}

read函数是阻塞的，所以执行时间就等于max＊time，即串行执行。可不可以非阻塞，就是readahead，此函数意思是在read之前，非阻塞的通知内核一下我要读的内容，内核会并发的预读这些内容进cache，当后续进行read时会大大的减少时间，代码修改成这样：

while (n < max) {
  readahead (offset);
}

while (n < max) {
  read (buf[i]);
  on_handle (buf[i]);
}

mmap

mmap的详细原理不在这里讨论，见图

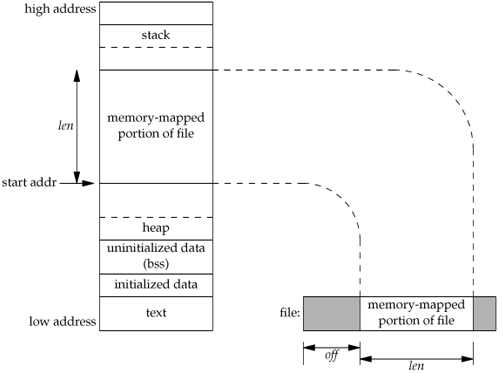
简单来说，是将内核空间映射到了用户空间，这样相比read函数来说减少了一次memcpy。

而mmap比O_DIRECT也有个好处是它确实利用了cache，可是对于普通的read来说，它利用的又不够充分，因为并不是每次访问都需要内核参与。不过有个补足办法就是用readahead，它可以传递你的意图(利用cache)给内核，从而避免了缺点。示例代码如下：

readahead (fd , offset);
ptr = mmap (fd);
a = ptr[offset];

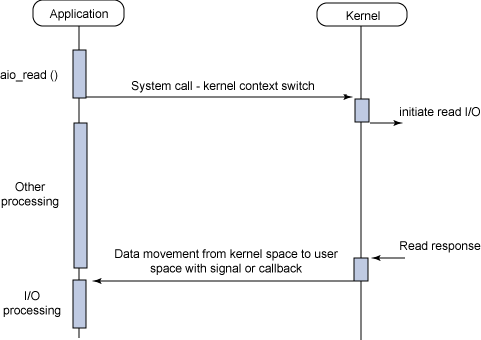
aio

从以上可以看出来，IO模式是从阻塞提升到了非阻塞，性能优化围绕着cache和memcpy，那有没有一种非阻塞的，有cache的，最少memcpy的，这些都符合的技术，那应该就是aio了吧，但Linux的aio到现在也没有一个很好的实现，也许过于复杂吧，反过来看下Window平台，这都真不是事。下图是aio模型：

Final

有了mmap＋ahead，aio真的还那么重要吗？真的很重要，没有真正的异步，就没有真正的并行编程，不能实现真正的async和await语法糖，比如一个异步方法要求10ms必须返回，而系统调用就得50ms完成，怎么可能是真正的async。但是如果不吹毛求疵，或追求极致的话，目前确实够用了，通过以上总结，希望能在IO编程时给你些选择素材。