Java实现常见查找算法

Java实现常见查找算法

查找是在大量的信息中寻找一个特定的信息元素，在计算机应用中，查找是常用的基本运算，例如编译程序中符号表的查找。

线性查找

线性查找（Linear Search）是一种简单的查找算法，用于在数据集中逐一比较每个元素，直到找到目标元素或搜索完整个数据集。它适用于任何类型的数据集，无论是否有序，但在大型数据集上效率较低，因为它的时间复杂度是 O(n)，其中 n 是数据集的大小。

以下是线性查找的基本步骤：

1. 从数据集的第一个元素开始，逐一遍历每个元素。
2. 比较当前元素与目标元素是否相等。
   • 如果相等，表示找到了目标元素，返回当前元素的索引位置。
   • 如果不相等，继续遍历下一个元素。
3. 如果遍历完整个数据集都没有找到目标元素，则返回一个表示元素不存在的标识（如 -1）。

以下是使用Java实现线性查找的示例代码：

public class LinearSearch {
    public static int linearSearch(int[] arr, int target) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == target) {
                return i; // 目标元素的索引位置
            }
        }
        return -1; // 目标元素不存在于数组中
    }

    public static void main(String[] args) {
        int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
        int target = 23;
        int result = linearSearch(arr, target);
        if (result == -1) {
            System.out.println("目标元素不存在于数组中");
        } else {
            System.out.println("目标元素的索引位置为: " + result);
        }
    }
}

二分查找

二分查找算法（Binary Search）是一种高效的查找算法，用于在有序数组或列表中查找特定元素的位置。它的基本思想是通过将数组分成两半，然后确定目标元素在哪一半，然后继续在那一半中搜索，重复这个过程直到找到目标元素或确定不存在。

二分查找算法的时间复杂度是 O(log n)，其中 n 是数据集的大小。这使得它在大型有序数据集中的查找操作非常高效,每次将数据集分成两半，然后确定目标元素在哪一半，然后继续在那一半中搜索。每次操作都将数据集的规模减少一半，因此它的时间复杂度是对数级别的.

需要注意的是，二分查找算法要求数据集必须是有序的。如果数据集无序，需要先进行排序操作。排序操作通常具有较高的时间复杂度（如快速排序的平均时间复杂度为 O(n log n)），因此总体上二分查找算法加上排序操作的时间复杂度可能会更高。

总结起来，二分查找算法是一种高效且常用的查找算法，在大型有序数据集中具有较低的时间复杂度。

以下是二分查找算法的详细步骤：

1. 初始化左指针 left 为数组的起始位置，右指针 right 为数组的结束位置。
2. 计算中间位置 mid，即 mid = left + (right - left) / 2。
3. 比较中间位置的元素与目标元素：
   • 如果中间位置的元素等于目标元素，则返回中间位置。
   • 如果中间位置的元素大于目标元素，则更新右指针 right = mid - 1，并回到步骤2。
     • 如果中间位置的元素小于目标元素，则更新左指针 left = mid + 1，并回到步骤2。
4. 如果左指针大于右指针，则表示目标元素不存在于数组中。

以下是使用Java实现二分查找算法的示例代码（迭代法）：

public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int left = 0;// 左指针，初始为数组起始位置
        int right = arr.length - 1;// 右指针，初始为数组结束位置

        while (left <= right) {
            int mid = left + (right - left) / 2; // 计算中间位置

            if (arr[mid] == target) { // 如果中间位置的元素等于目标元素，则找到目标元素
                return mid;
            } else if (arr[mid] < target) { // 如果中间位置的元素小于目标元素，则在右半部分继续查找
                left = mid + 1;
            } else {  // 如果中间位置的元素大于目标元素，则在左半部分继续查找
                right = mid - 1;
            }
        }

        return -1; // 目标元素不存在于数组中

递归法

public class BinarySearchRecursive {
    public static int binarySearch(int[] arr, int target, int left, int right) {
        if (left <= right) {
            int mid = left + (right - left) / 2;// 计算中间位置

            if (arr[mid] == target) {
                return mid;
            } else if (arr[mid] < target) {// 如果中间位置的元素小于目标元素，则在右半部分继续查找
                return binarySearch(arr, target, mid + 1, right);
            } else {// 如果中间位置的元素大于目标元素，则在左半部分继续查找
                return binarySearch(arr, target, left, mid - 1);
            }
        }

        return -1; // 目标元素不存在于数组中
    }

    public static void main(String[] args) {
        int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
        int target = 23;
        int result = binarySearch(arr, target, 0, arr.length - 1);

        if (result == -1) {
            System.out.println("目标元素不存在于数组中");
        } else {
            System.out.println("目标元素的索引位置为: " + result);
        }
    }
}

如果数组中有多个相同的目标元素，上面的算法只会返回其中一个的索引位置，可以优化一下返回全部元素的下标

// 迭代
public static List<Integer> binarySearchAllIterative(int[] arr, int target) {
    List<Integer> indices = new ArrayList<>();
    int left = 0;
    int right = arr.length - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) {
            indices.add(mid);

            // 向左扫描找到所有相同元素的索引
            int temp = mid - 1;
            while (temp >= 0 && arr[temp] == target) {
                indices.add(temp);
                temp--;
            }

            // 向右扫描找到所有相同元素的索引
            temp = mid + 1;
            while (temp < arr.length && arr[temp] == target) {
                indices.add(temp);
                temp++;
            }

            break; // 结束循环，避免重复扫描
        } else if (arr[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return indices;
}

// 递归
public class BinarySearchMultiple {
    public static List<Integer> binarySearchAll(int[] arr, int target) {
        List<Integer> indices = new ArrayList<>();
        binarySearchAllRecursive(arr, target, 0, arr.length - 1, indices);
        return indices;
    }

    public static void binarySearchAllRecursive(int[] arr, int target, int left, int right, List<Integer> indices) {
        if (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] == target) {
                indices.add(mid); // 将找到的索引加入列表
                // 继续在左半部分和右半部分继续查找相同目标元素的索引
                binarySearchAllRecursive(arr, target, left, mid - 1, indices);
                binarySearchAllRecursive(arr, target, mid + 1, right, indices);
            } else if (arr[mid] < target) {
                binarySearchAllRecursive(arr, target, mid + 1, right, indices);
            } else {
                binarySearchAllRecursive(arr, target, left, mid - 1, indices);
            }
        }
    }
}

通常情况下，迭代法比递归法的效率要高。这是因为迭代法避免了函数调用的开销，而函数调用涉及堆栈管理、参数传递等操作，会导致一定的性能损耗。此外，迭代法通常更容易优化，可以通过使用循环不断更新变量的方式来进行计算，从而更有效地利用计算资源。

插值查找

插值查找算法是一种基于有序数组的搜索算法，类似于二分查找，但它在选择比较的元素时使用了一种更为精细的估计方法，从而更接近目标元素的位置。插值查找的基本思想是根据目标元素的值与数组中元素的分布情况，估算目标元素在数组中的大致位置，然后进行查找。

在二分查找中，mid的计算方式如下：

\[mid = \frac{low+high}{2}
\]

将low从分数中提取出来，mid的计算就变成了：

\[mid =low + \frac{low+high}{2}
\]

在插值查找中，mid的计算方式转换成了：

\[mid =low + \frac{key-a[low] }{a[high] - a[low]}(high-low)
\]

low 表示左边索引left, high表示右边索引right,key 就是target

插值查找算法的步骤如下：

1. 初始化左指针 left 为数组的起始位置，右指针 right 为数组的结束位置。
2. 使用插值公式来估算目标元素的位置：
   
   pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left])
   
   其中，target 是目标元素的值，arr[left] 和 arr[right] 分别是当前搜索范围的左边界和右边界的元素值。
3. 如果估算位置 pos 对应的元素值等于目标元素 target，则找到目标元素，返回位置 pos。
4. 如果估算位置 pos 对应的元素值小于目标元素 target，则说明目标元素在当前位置的右侧，更新 left = pos + 1。
5. 如果估算位置 pos 对应的元素值大于目标元素 target，则说明目标元素在当前位置的左侧，更新 right = pos - 1。
6. 重复步骤 2 到步骤 5，直到找到目标元素或搜索范围缩小到无法继续搜索为止。

插值查找的优势在于当数组元素分布均匀且有序度较高时，其效率可以比二分查找更高。然而，当数组元素分布不均匀或有序度较低时，插值查找可能会导致性能下降，甚至变得不如二分查找。

需要注意的是，插值查找算法的时间复杂度通常为 O(log log n)，但在某些特殊情况下，可能会退化为 O(n)。因此，在选择搜索算法时，需要根据具体的数据分布情况和性能需求进行考虑。

插值查找算法的示例代码：

public class InterpolationSearch {
    /**
     * 插值查找算法
     *
     * @param arr    有序数组
     * @param target 目标元素
     * @return 目标元素在数组中的索引位置，如果不存在则返回 -1
     */
    public static int interpolationSearch(int[] arr, int target) {
        int left = 0; // 左指针，初始为数组起始位置
        int right = arr.length - 1; // 右指针，初始为数组结束位置

        while (left <= right && target >= arr[left] && target <= arr[right]) {
            // 使用插值公式估算目标元素的位置
            int pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left]);

            if (arr[pos] == target) {
                return pos; // 找到目标元素
            }

            if (arr[pos] < target) {
                left = pos + 1; // 目标元素在右半部分
            } else {
                right = pos - 1; // 目标元素在左半部分
            }
        }
        return -1; // 目标元素不存在于数组中
    }

    public static void main(String[] args) {
        int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
        int target = 23;
        int result = interpolationSearch(arr, target);
        if (result == -1) {
            System.out.println("目标元素不存在于数组中");
        } else {
            System.out.println("目标元素的索引位置为: " + result);
        }
    }
}

斐波那契查找

斐波那契查找是一种基于黄金分割原理的查找算法，它是对二分查找的一种改进。斐波那契查找利用了斐波那契数列的特性来确定查找范围的分割点，从而提高了查找效率。

随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中，斐波那契查找原理与前两种相似，仅仅改变了中间结点（mid）的位置，mid不再是中间或插值得到，而是位于黄金分割点附近，即mid=low+F(k-1)-1（F代表斐波那契数列）

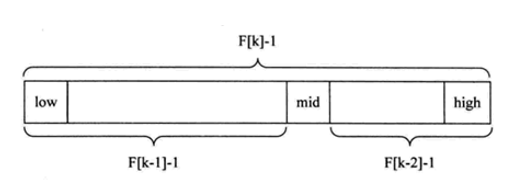
斐波那契查找的基本思想如下：

1. 首先，需要准备一个斐波那契数列，该数列满足每个元素等于前两个元素之和。例如：0, 1, 1, 2, 3, 5, 8, 13, ...

2. 初始化左指针 left 和右指针 right 分别指向数组的起始位置和结束位置。

3. 根据数组长度确定一个合适的斐波那契数列元素作为分割点 mid，使得 mid 尽可能接近数组长度。

4. 比较目标元素与分割点mid

   对应位置的元素值：

   • 如果目标元素等于 arr[mid]，则找到目标元素，返回位置 mid。
   • 如果目标元素小于 arr[mid]，则说明目标元素在当前位置的左侧，更新右指针为 mid - 1。
   • 如果目标元素大于 arr[mid]，则说明目标元素在当前位置的右侧，更新左指针为 mid + 1。

5. 重复步骤 3 和步骤 4，直到找到目标元素或搜索范围缩小到无法继续搜索为止。、

斐波那契查找的优势在于它能够更快地确定分割点，从而减少了比较次数。它的时间复杂度为 O(log n)，与二分查找相同。然而，斐波那契查找需要预先计算斐波那契数列，并且在每次查找时都需要重新确定分割点，因此在实际应用中可能会带来一定的额外开销。

需要注意的是，斐波那契查找适用于有序数组，并且数组长度较大时效果更好。对于小规模的数组或者无序数组，二分查找可能更适合。

代码示例：

public class FibonacciSearch {

    public static int maxSize = 20;
    public static void main(String[] args) {
        int [] arr = {1,4, 10, 69, 1345, 6785};

        System.out.println("index=" + fibSearch(arr, 1345));// 0

    }

    // 生成 斐波那契数列
    public static int[] fib() {
        int[] f = new int[20];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }

    /**
     *
     * @param a  数组
     * @param key 我们需要查找的关键码(值)
     * @return 返回对应的下标，如果没有-1
     */
    public static int fibSearch(int[] a, int key) {
        int low = 0;
        int high = a.length - 1;
        int k = 0; //表示斐波那契分割数值的下标
        int mid = 0; //存放mid值
        int f[] = fib(); //获取到斐波那契数列
        //获取到斐波那契分割数值的下标
        while(high > f[k] - 1) {
            k++;
        }
        //因为 f[k] 值 可能大于 a 的 长度，因此我们需要使用Arrays类，构造一个新的数组，并指向temp[]
        //不足的部分会使用0填充
        int[] temp = Arrays.copyOf(a, f[k]);
        //实际上需求使用a数组最后的数填充 temp
        for(int i = high + 1; i < temp.length; i++) {
            temp[i] = a[high];
        }

        while (low <= high) { // 只要这个条件满足，就可以找
            mid = low + f[k - 1] - 1;
            if(key < temp[mid]) { //我们应该继续向数组的前面查找(左边)
                high = mid - 1;
                //说明
                //1. 全部元素 = 前面的元素 + 后边元素
                //2. f[k] = f[k-1] + f[k-2]
                //因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]
                //即 在 f[k-1] 的前面继续查找 k--
                //即下次循环 mid = f[k-1-1]-1
                k--;
            } else if ( key > temp[mid]) { // 我们应该继续向数组的后面查找(右边)
                low = mid + 1;
                //1. 全部元素 = 前面的元素 + 后边元素
                //2. f[k] = f[k-1] + f[k-2]
                //3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4]
                //4. 即在f[k-2] 的前面进行查找 k -=2
                //5. 即下次循环 mid = f[k - 1 - 2] - 1
                k -= 2;
            } else { //找到
                //需要确定，返回的是哪个下标
                if(mid <= high) {
                    return mid;
                } else {
                    return high;
                }
            }
        }
        return -1;
    }
}

哈希查找

哈希查找算法（Hashing）是一种用于高效查找数据的算法，它将数据存储在散列表（Hash Table）中，并利用散列函数将数据的关键字映射到表中的位置。哈希查找的核心思想是通过散列函数将关键字转换为表中的索引，从而实现快速的查找操作。

在平均情况下，哈希查找的时间复杂度可以达到O(1)。但是，在最坏情况下，哈希查找的时间复杂度可能会退化到O(n)，其中n是散列表中存储的键值对数量

Java提供了用于实现哈希表（散列表）的数据结构，这就是HashMap类。HashMap是Java标准库中最常用的哈希表实现之一，用于存储键值对，并提供了快速的查找、插入和删除操作。

通过leetcode第一题两数之和可以了解哈希表的使用

代码示例

public static int[] twoSum(int[] nums, int target) {

    int[] indexs = new int[2];

    HashMap<Integer, Integer> hashMap = new HashMap<>();

    for (int i = 0; i < nums.length; i++) {

        if (hashMap.containsKey(nums[i])){
            indexs[0] = i;
            indexs[1] = hashMap.get(nums[i]);
            return indexs;
        }

        hashMap.put(target - nums[i],i);
    }
    return indexs;

}

二叉树查找

二叉搜索树是一种特殊的二叉树，它是一种有序的树结构，可以用于实现二叉树查找。在二叉搜索树中，对于每个节点，其左子树的值都小于该节点的值，而右子树的值都大于该节点的值。这种结构使得在二叉搜索树中可以快速地进行查找操作。

详细看这篇文章 二叉搜索树