[C++]线段树 区间修改 单点查询

线段树 区间修改 单点查询

请先阅读上一篇Bolg

算法思想

由于是区间修改

那就把下放的每一个线段给套上一层标记

来表达增加的值

单点查询就把那些标记穿起来就行了

当然 还要加上那原来的值

来举个例子：

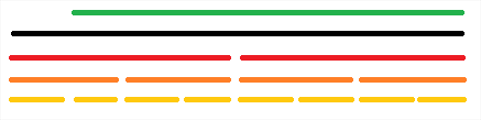
我想要更改绿色这段区间的值

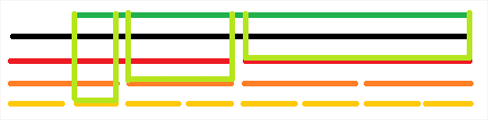
那就在绿色这段上下推标记

然后我又想在蓝色这段上更改区间值

那就继续下推标记

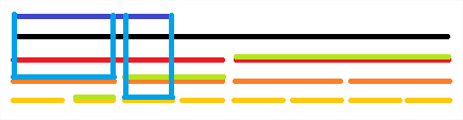
如果我想要查询紫色的这个点的值

那就把一路上的标记(绿色和蓝色的)加起来

最后再把那个点原本的值加起来(黄色那一小段)

就是最终的值了

代码实现

变量含义详见上个Blog

有个新变量就是那个标记

就是 Node 结构体中的 k

Build函数和上个相同

添加标记

void add(int i,int l,int r,int k){
	if(l <= tree[i].l && tree[i].r <= r){
		tree[i].k += k;
		return ;
	}
	if(tree[li].r >= l)
		add(li,l,r,k);
	if(tree[ri].l <= r)
		add(ri,l,r,k);
}

• \(l <= tree[i].l\) && \(tree[i].r <= r\)

这代表这个线段已经完全被包围了

那就把这个线段打上标记

并且要停止继续向下打标记

因为这段已经打上了

所以 \(return ;\)

• \(tree[li].r >= l\)
• \(tree[ri].l <= r\)

这里和上个相同

哪有搜哪里

单点查询

int search(int i,int dis,int ans){
	if(tree[i].l == tree[i].r){
		return val[dis] + tree[i].k;
	}
	if(dis <= tree[li].r)
		return tree[i].k + search(li,dis,ans);
	if(dis >= tree[ri].l)
		return tree[i].k + search(ri,dis,ans);
}

• \(tree[i].l == tree[i].r\)

已经查询到点了

那就返回点的值和这个线段上的标记

• \(dis <= tree[li].r\)
• \(dis >= tree[ri].l\)

如果没有到点

那就加上这个线段的标记

以及继续往下搜的结果

线段数 区间修改 区间查询

Code

#include<bits/stdc++.h>
#define maxn 1000010
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
using namespace std;

int n,val[maxn];

struct Node{
	int l,r,sum,k;
}tree[maxn];

void Read(){
	cin >> n;
	for(int i = 1;i <= n;i++)cin >> val[i];
}

void build(int i,int l,int r){
	tree[i].l = l;
	tree[i].r = r;
	if(l == r){
		tree[i].sum = val[l];
		return ;
	}
	build(li,l,mid);
	build(ri,mid+1,r);
	tree[i].sum = tree[li].sum + tree[ri].sum;
	return ;
}

void add(int i,int l,int r,int k){
	if(l <= tree[i].l && tree[i].r <= r){
		tree[i].k += k;
		return ;
	}
	if(tree[li].r >= l)
		add(li,l,r,k);
	if(tree[ri].l <= r)
		add(ri,l,r,k);
}

int search(int i,int dis,int ans){
	if(tree[i].l == tree[i].r){
		return val[dis] + tree[i].k;
	}
	if(dis <= tree[li].r)
		return tree[i].k + search(li,dis,ans);
	if(dis >= tree[ri].l)
		return tree[i].k + search(ri,dis,ans);
}

void interaction(){
	while(1){
		int tot;
		cin >> tot;
		if(tot == 1){
			int dis;
			cin >> dis;
			cout << search(1,dis,0) << endl;
		} else if(tot == 2){
			int l,r,k;
			cin >> l >> r >> k;
			add(1,l,r,k);
		} else if(tot == 3){
			return ;
		}
	}
}

int main(){
	cout << "query point" << endl << "change section" << endl;
	Read();
	build(1,1,n);
	cout << "query 1" << endl << "change 2" << endl << "break 3" << endl;
	interaction();
	return 0;
}