题解 P9326

前言

数学符号约定

\(n\)：任意正整数。

\(\#\)：从未出现过的小写字母。

\(\Sigma\)：字符集，这里指小写字母集合。

\(S\)：最终答案的字符矩阵。

其余符号同题目翻译中所写。

如非特殊说明，将会按照上述约定书写符号。

题目大意

构造一个 \(N\times M\) 的小写字母矩阵，使得其中有 \(R\) 行 \(C\) 列是回文串，如果无解，输出 IMPOSSIBLE。

题目分析

首先，让我们仔细阅读一下题目，然后可以得到一个比较显然的性质，就是在 \(R\lt N\) 和 \(C \lt M\) 的时候我们行回文串与列回文串的位置是不重要的，也就是位置无关，可以放到任意位置。证明比较显然，考虑我们如果想要满足任意列数 \(C\;(C\lt N)\) 的话至多会使得一行无法形成回文串，但是此时目标要求 \(R \lt N\) 即 \(R_{\max} = N-1\)，所以能够达到题目要求。

所以，我们现在考虑一下 \(R\lt N\) 且 \(C \lt M\) 的情况下怎么填。考虑让我们的回文串填的暴力一点，即全都填一个字符，这个时候我们预期达到的效果如图所示：

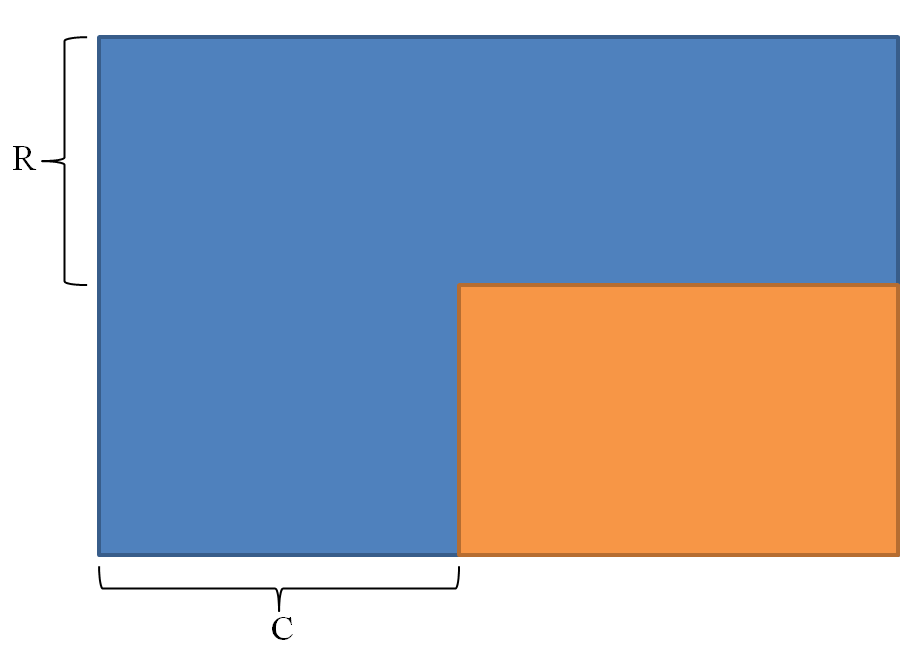
其中，蓝色部分全填的字符 \(\#\)，橙色部分所填字符比较复杂，它的填写规则是这样的：

对于第 \(i\) 行第 \(j\) 列（这里的 \(i,\,j\) 是相对于橙色矩形的第 \(i\) 行第 \(j\) 列）填写字符 \((i+j) \bmod (|\Sigma| - 1)\)。

可以证明，根据上述填写方法，能够保证第 \(R+1 \sim N\) 行和第 \(C+1\sim M\) 列不会出现回文串，理由如下：

考虑回文串的定义，如果我们想让第 \(i\) 行字符串为回文串，则需要满足下面条件：

\[\forall j \in [1,M]\qquad S_{i,j} = S_{i,M-j+1}
\]

现在我们 \(S_{i,j}\) 位置上的字符进行分类讨论：

1. 如果 \(S_{i,j} = \#\)，则显然当前字符串不为回文串，理由如下：

   如果 \(S_{i,j} = \#\) 且 \(S_{i,j} = S_{i,M-j+1}\)，由于橙色部分不可能出现 \(\#\)，则说明 \(C = M\)，不符合前置条件 \(C\lt M\)，故不成立。

2. 如果 \(S_{i,j} \not= \#\)，则说明 \(C=0\)，那么证明 \(S_{i,j} = S_{i,M-j+1}\)，就等价于证明：

   \[\forall j\in [1,M]\qquad i+j \equiv i+M-j+1 \pmod{|\Sigma| -1}
   \]

   移项，可以得到：

   \[\forall j\in [1,M]\qquad 2j \equiv M+1 \pmod{|\Sigma|-1}
   \]

   考虑将同余式转化为线性不定方程：

   \[2j + (|\Sigma| - 1)y = M+1
   \]

   根据裴蜀定理，若我们想要方程组有解，则需要满足 \(\gcd(2,|\Sigma| - 1) \mid (M+1)\)，由于 \(\gcd(2,|\Sigma| - 1) = \gcd(2,25) = 1\)，所以原线性不定方程有解。

   那么此时，我们假设最小的解 \(j_0 \in [1,M]\)，根据裴蜀定理可知，上述不定方程关于 \(j\) 的解集 \(J = \{j_t|j_t = j_0 + (|\Sigma| - 1)t,\, t\in [0,+\infty)\}\)，那么我们现在证明的命题就变为：

   \[[1,M]\subset J
   \]

   若该命题成立，则显然需要 \(|\Sigma| - 1 = 1\) 即 \(|\Sigma| = 2\)，这与我们的条件 \(|\Sigma| = 26\) 不符，故命题不成立。

最后，根据当前的构造方案可以看出，证明列不出现回文串只需要证明行不出现即可，因为我们在第 \(i\) 行第 \(j\) 列所填字符为 \((i+j) \bmod (|\Sigma|-1)\)，顺时针或逆时针旋转 \(90^{\circ}\) 本质上就是 \(i\) 与 \(j\) 发生交换，因为加法满足交换律，所以我们从行得到的结论可以用于列上。

接下来，我们就需要处理 \(R = N\) 或 \(C = M\) 的情况了：

先考虑 \(R = N\) 的情况，因为 \(C = M\) 的情况就是沿顺时针或逆时针旋转 \(90^{\circ}\) 而已。

如果我们想在不破坏某一行为回文串的情况下达成 \(C\) 列为回文串的目标，则显然列与列的位置一定是对称的，换句话说，倘若第 \(c\) 列为回文串，则必然 \(M - c + 1\) 这一列也为回文串。

那么不难得出结论，当 \(M\) 为奇数的时候，可以构造出任意的 \(C\)，当 \(M\) 为偶数的时候，可以构造出偶数的 \(C\)，构造方案考虑最后一行中，让对称的 \(c\) 的位置填 \(\#\)，其余位置填字符 \(x\,(x \not = \#)\)，即构成如下情况：

\[\begin{aligned}
&\text{奇数且 } C \text{ 为奇数：}\\
& \#\,\cdots \, x\,\cdots\, x\,\#\,x\cdots \# \cdots \#\\
&\text{其余情况：}\\
& \#\,\cdots \, x\,\cdots\, x\,\cdots \,\# \,\cdots \,\#\\
\end{aligned}
\]

综上，我们做完了本题

代码实现

这里给出了关键部分的代码实现，其余部分还恳请读者自己完成：

const char sharp = 'z';
char ansmap[MAX_SIZE][MAX_SIZE];

void main(){
	int N = read();
	int M = read();
	int R = read();
	int C = read();
	if(R == N && C == M){
		for(int i=1;i<=N;i++){
			for(int j=1;j<=M;j++){
				printf("%c",sharp);
			}
			printf("\n");
		}
	} else if(R == N || C == M) {
		int flag = 0;
		if(C == M){
			swap(N,M);
			swap(R,C);
			flag = 1;
		}
		if(!(M & 1) && (C & 1)){
			printf("IMPOSSIBLE");
			return ;
		}
		for(int i=1;i<N;i++){
			for(int j=1;j<=M;j++){
				ansmap[i][j] = sharp;
			}
		}
		char x = 'y';
		int i = 1;
		while(C > 1){
			ansmap[N][i] = sharp;
			ansmap[N][M-i+1] = sharp;
			i++;
			C -= 2;
		}
		if(C){
			ansmap[N][(M >> 1) + 1] = sharp;
		}
		for(i=1;i<=M;i++){
			if(ansmap[N][i] != sharp){
				ansmap[N][i] = x;
			}
		}
		if(flag)
			swap(N,M);
		printmat(N,M,flag);
	} else {
		for(int i=1;i<=R;i++){
			for(int j=1;j<=M;j++){
				ansmap[i][j] = sharp;
			}
		}
		for(int i=1;i<=N;i++){
			for(int j=1;j<=C;j++){
				ansmap[i][j] = sharp;
			}
		}
		for(int i=R+1;i<=N;i++){
			for(int j=C+1;j<=M;j++){
				ansmap[i][j] = ((i+j)%25) + 'a';
			}
		}
		printmat(N,M);
	}
}