二叉树、平衡二叉树、红黑树、B树、B+树

• 几种树的主要区别：

  • 红黑树为二叉自平衡搜索树，深度大，多用于内存排序；

  • B树为多路（多叉）搜索树，深度低，搜索数据时磁盘IO较少，多用于索引外存数据，只支持随机访问，不支持顺序访问；

  • B+树是对B树的改进，内节点不保存数据地址指针（可保存更多关键字），内节点可看做为外节点的索引，所有数据地址存储在外节点，数据搜索效率一致。外节点依关键字组成顺序链表，支持区间搜索，且空间局部性好，缓存命中率高；

• 二叉树
  • 基于二叉查找树的这种特点，在查找某个节点的时候，可以采取类似于二分查找的思想，快速找到某个节点。n 个节点的二叉查找树，正常的情况下，查找的时间复杂度为 O(logN)。
  • 

  • 二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序时，例如序列 A = {1，2，3，4，5，6}，构造二叉搜索树如图 1.1。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 O(n)。

    

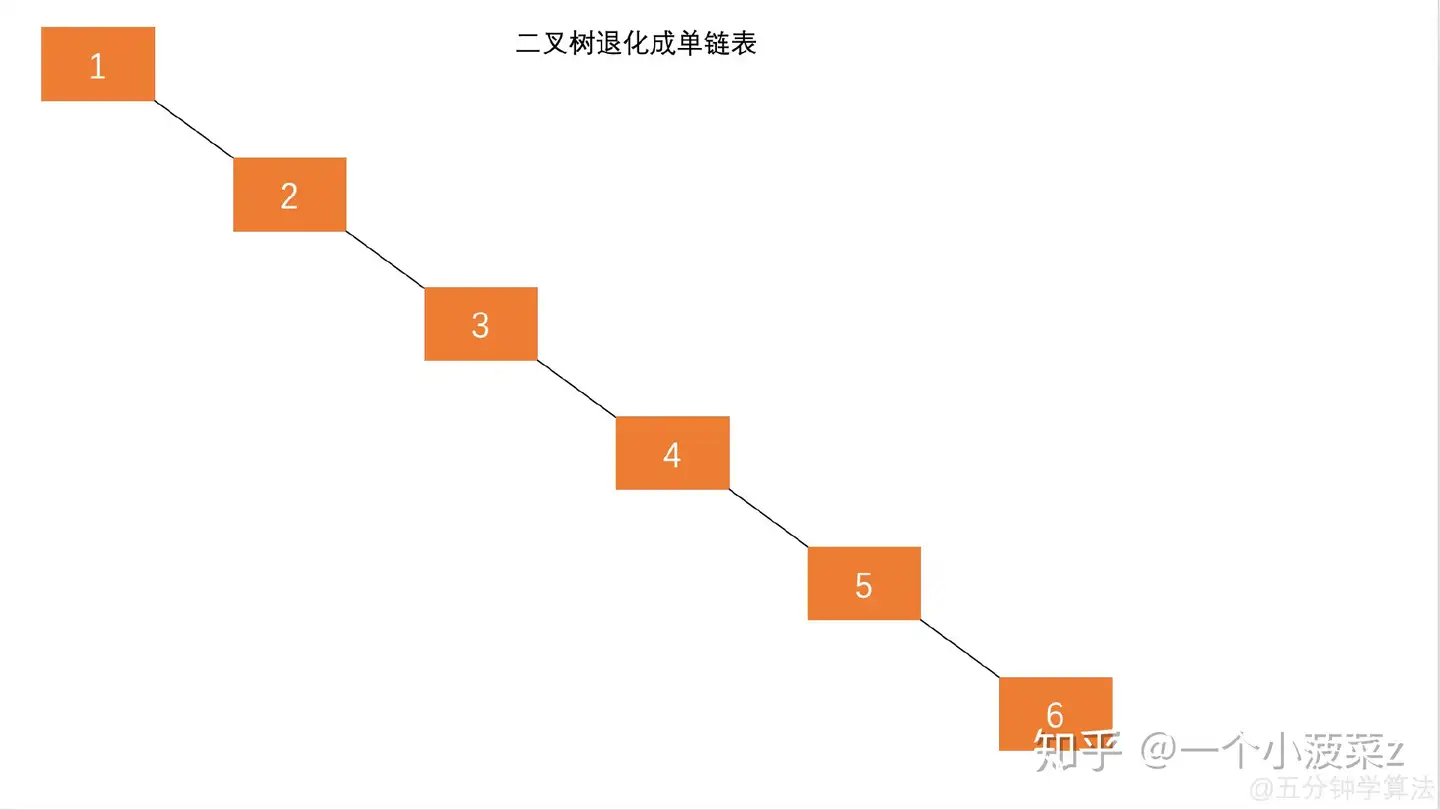
    在此二叉搜索树中查找元素 6 需要查找 6 次。

• 平衡二叉树

  • 平衡二叉树是基于二分法的策略提高数据的查找速度的二叉树的数据结构。平衡二叉树是采用二分法思维把数据按规则组装成一个树形结构的数据，用这个树形结构的数据减少无关数据的检索，大大的提升了数据检索的速度。定义如下：

    • 可以是空树。
    • 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。
  • 问题：
    • 为什么有了平衡树还需要红黑树？
      　虽然平衡树解决了二叉查找树退化为近似链表的缺点，能够把查找时间控制在 O(logn)，不过却不是最佳的，因为平衡树要求每个节点的左子树和右子树的高度差至多等于1，这个要求实在是太严了，导致每次进行插入/删除节点的时候，几乎都会破坏平衡树的第二个规则，进而都需要通过左旋和右旋来进行调整，使之再次成为一颗符合要求的平衡树。
  • 例子
  • 

    

• 红黑树

  • 显然，如果在插入、删除很频繁的场景中，平衡树需要频繁调整，这会使平衡树的性能大打折扣，为了解决这个问题，于是有了红黑树，红黑树具有如下特点：

    • 每个节点或者是黑色，或者是红色。
    • 根节点是黑色。
    • 每个叶子节点(NIL)是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点]
    • 如果一个节点是红色的，则它的子节点必须是黑色的。
    • 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。[这里指到叶子节点的路径]

  • 包含n个内部节点的红黑树的高度是 O(log(n))。如图：

    

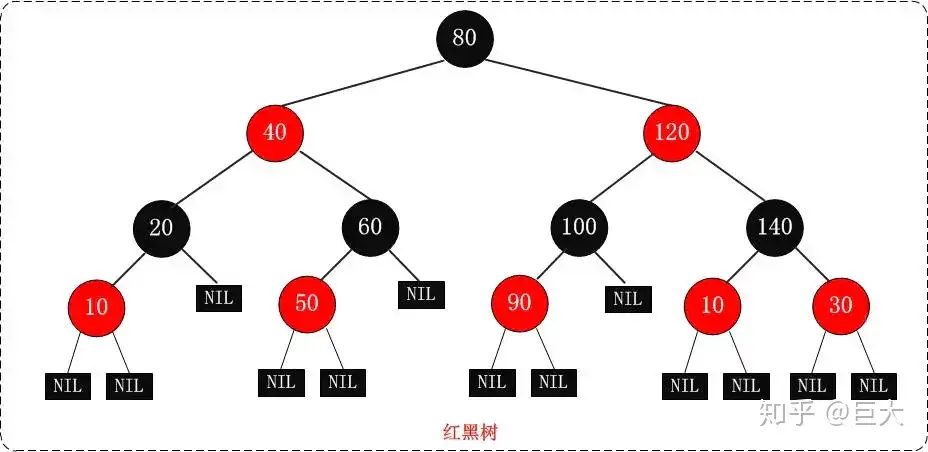
  • 3、红黑树的使用场景
    java中使用到红黑树的有TreeSet和JDK1.8的HashMap。红黑树的插入和删除都要满足以上5个特性，操作非常复杂，为什么要使用红黑树？
  • 原因：
    红黑树是一种平衡树，复杂的定义和规则都是为了保证树的平衡性。
• B树
  • B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个)，数据库索引技术里大量使用B树和B+树的数据结构。
  • 查找E的流程
    • 如要从上图中找到E，查找流程如下：

      （1）获取根节点的关键字进行比较，当前根节点关键字为M，E<M(26个字母顺序)，所以往找到指向左边的子节点(二分法规则，左小右大，左边放小于当前节点值的子节点、右边放大于当前节点值的子节点)。

      （2）拿到关键字D和G，D<E<G 所以直接找到D和G中间的节点。

      （3）拿到E和F，因为E=E，所以直接返回关键字和指针信息(如果树结构里面没有包含所要查找的节点则返回null)。

  • 

    

• B+树
  • B+树有两种类型的节点：内部结点（也称索引结点）和叶子结点。内部节点就是非叶子节点，内部节点不存储数据，只存储索引，数据都存储在叶子节点。
  • 内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
  • 每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接。
  • 父节点存有右孩子的第一个元素（叶子节点）的索引。
  • 
  • 

参考文献

　　https://cloud.tencent.com/developer/article/1691641

https://segmentfault.com/a/1190000020416577

https://zhuanlan.zhihu.com/p/56066942

https://zhuanlan.zhihu.com/p/342539584

      https://blog.csdn.net/sinat_34072381/article/details/107197754