Leetcode刷题笔记——单调性

单调性

单调性是数学中使用的一种常见性质，通常用于描述函数，在高等数学中的定义常常为：

设函数f(x)在区间I上有定义，如果对于I上的任意两个数x1和x2，当x1<x2时，有f(x1)<f(x2)（或者f(x1)>f(x2)），则称函数f(x)在区间I上是单调递增的（或者单调递减的）。

例如如下图像就是两个单调函数。

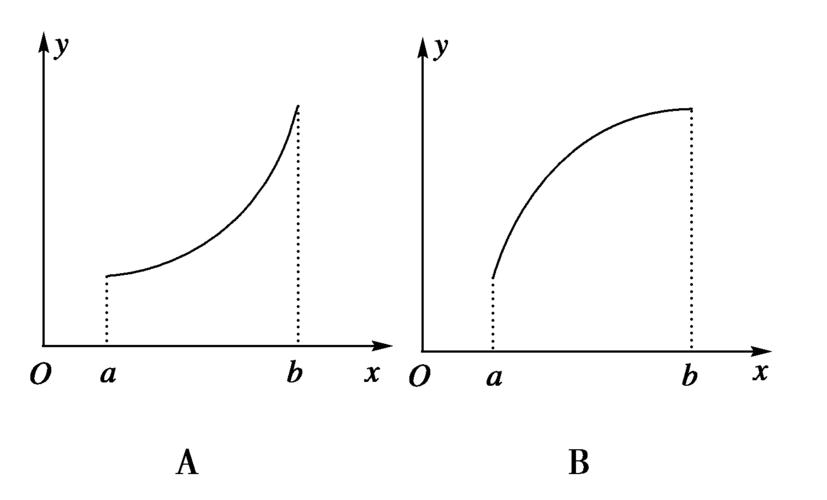
利用单调性我们可以减少很多重复的运算。例如，对于如下函数，我们给定其定义域为[0,+∞)，现在要求查找出在其定义域内所有f(x)即y大于0.5的区间。

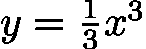
• 如果不借助单调性，我们需要采用遍历的方法，依次遍历定义域中的所有点x，判断其f(x)是否满足条件（大于0.5）。
• 如果借助单调性，我们知道上述函数是严格单调递增的，其图像如下：
  
  
  
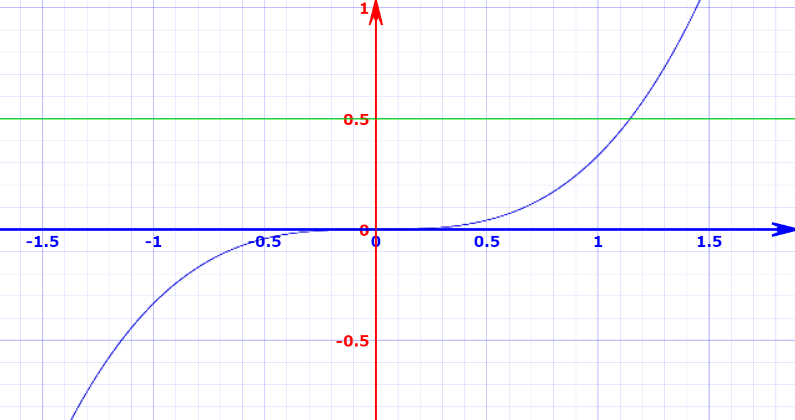
  绿线表示y=0.5的图像，处理该问题，只需要找到方程0.5=(1/3)x^3的解x0，由于函数具有单调性，且单调递增，因此，所有大于x0的区间内的x其f(x)都满足大于0.5。

对于计算机语言来说，用于表示函数的常见数据结构就是数组，我们可以通过

1. 原数组本身的单调性
2. 构造单调性

简化许多运算。下面引入几个例子:

15. 三数之和

823. 带因子的二叉树

15. 三数之和

题目：给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：

1. 答案中不可以包含重复的三元组
2. 3 <= nums.length <= 3000
3. -10^5 <= nums[i] <= 10^5

按照最朴素的解决方法，三层循环，循环遍历整个数组，然后再对整个结果进行去重，便可以解决该问题，但是时间复杂度为O(n^3)，由于过于简单，这里给出伪代码：

list = [][]int{}
for i:=0;i <= len(nums)-3;i ++ {
  for j:=i+1;j <= len(nums)-2;j ++ {
    for k:= j+1;k < len(nums)-1;k ++ {
      if nums[i]+nums[j]+nums[k] == 0 {
        list = append(list, []int{nums[i],nums[j],nums[k]})
      }
    }
  }
}
对list去重

本题目首先要求我们去重，因为返回结果要求不重复，对于去重常见的做法：

1. 使用数据结构set、map进行处理，但是会额外占用内存
2. 对原始数据排序，然后按序处理跳过重复项

优化掉去重问题后，我们可以尝试对内层的两层for循环进行优化，这里就引入了一个经典的方法：构造单调性，根据单调性进行查找。

巧妙的方法

如果nums[i]确定，那么我们只需要寻找满足条件nums[j]+nums[k]=-nums[i]的j、k值，这就变成了一个二数之和的问题，暴力算法是直接进行遍历，然后查找该值，但是由于数组的有序性，我们有一种更加巧妙的方法：

• 由于当前数组的有序性，保证了数组本身是单调递增（或递减的，这里以递增为例）
• 设置指针p1、p2指向数组开头p1=i+1和结尾p2=len(nums)-1
• pred=nums[p1]+nums[p2],target=-nums[i]
  • if target < pred，由于数组递增，nums[p2-1]<num[p2]，因此，p2 --
  • if target > pred，由于数组递增，nums[p1+1]>num[p1]，因此，p1 ++
  • if target == pred，找到了目标，但为防止遗漏数据还要继续查找，此时指针向任意方向移动都没有影响，可以p1 ++或者p2 --
• 直到p1 >p2则可以停止查找(=取决于需求，如果有需求可以>=或<=)

这个模式可以应用于很多地方，实际上具有单调性的函数一般都可以通过该办法查找，例如nums[j]*nums[k]=target，查找j、k。

例如，在[-1,0,1,2,-1, 3]这个数组中，查找nums[j]+nums[k]=4的nums[j]和nums[k]的值，现对其进行排序，然后用上述方法进行处理：

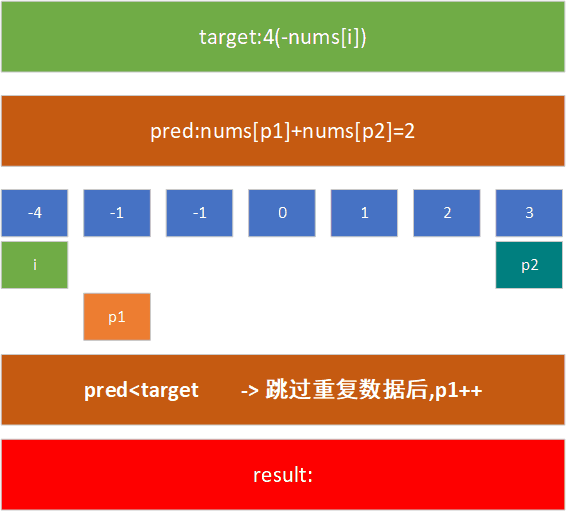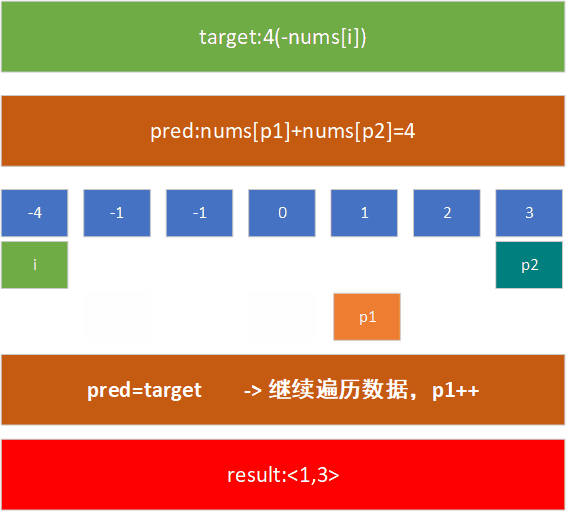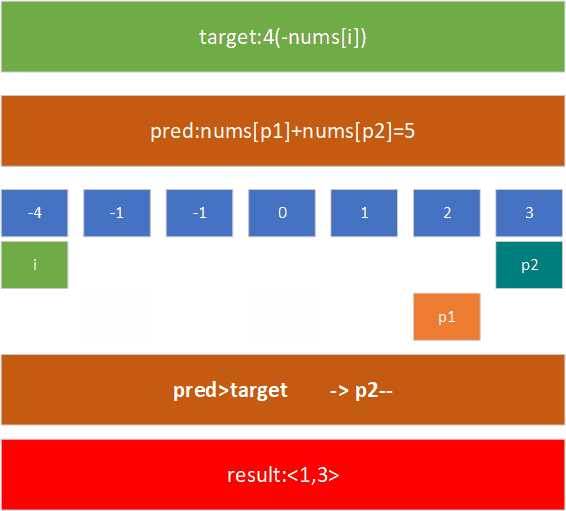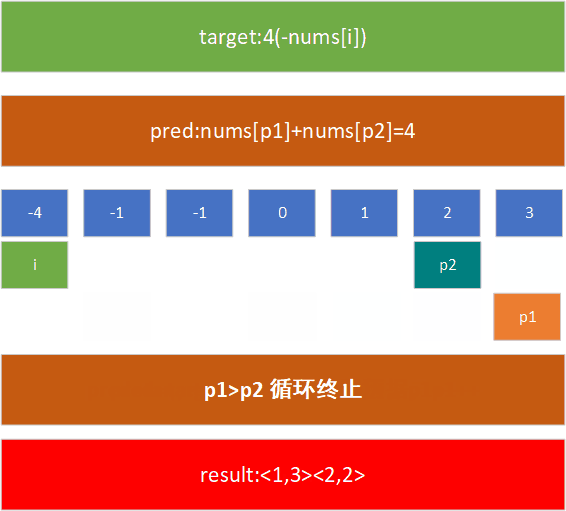
了解了这个模式后，我们给出解决该问题的代码：

解题代码以及注释

import "sort"

func threeSum(nums []int) [][]int {
	result := [][]int{}
	sort.Ints(nums)
    // 尝试固定i，然后将3数之和转化为两数之和
	for i := 0; i < len(nums)-2; i++ {
        // 对nums[i]进行去重
		if i-1 >= 0 && nums[i-1] == nums[i] {
			continue
		}
		sum := -nums[i]
		left := i + 1
		right := len(nums) - 1
        // 解决两数之和问题，寻找left、right使得nums[left]+nums[right]==sum
		for left < right {
			temp := nums[left] + nums[right]
			if temp == sum {
				result = append(result, []int{nums[i], nums[left], nums[right]})
                // 去重nums[left]
				for left < right && nums[left] == nums[left+1] {
					left++
				}
                // 去重nums[right]
				for left < right && nums[right] == nums[right-1] {
					right--
				}
				left++
				right--
			} else if temp > sum {
				right--
			} else {
				left++
			}
		}
	}
	return result
}

823. 带因子的二叉树

题目：给出一个含有不重复整数元素的数组arr，每个整数arr[i]均大于 1。用这些整数来构建二叉树，每个整数可以使用任意次数。其中：每个非叶结点的值应等于它的两个子结点的值的乘积。满足条件的二叉树一共有多少个？答案可能很大，返回 对 10^9+7 取余 的结果。

例如：输入: arr = [2, 4, 5, 10]

输出: 7

解释: 可以得到这些二叉树: [2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2]

该问题是一个树相关的问题，并且对于父子结点处理过程是类似的。举例说明这件事：

对于输入arr=[18, 3, 6, 2]，页结点可以为[2][3][6][18]，可以把未显示的结点看做空结点，对于顶点为6的树可以为[6,2,3]或者[6,3,2]，就需要借助叶节点信息。对于顶点为18的树可以为[18,3,6],[18,6,3]，而组成以[6]的顶点的组合有3个。可以看到该问题是个动态规划问题。

f(18)=f(3)*f(6)
f(18)=f(6)*f(3)
f(6)=f(3)*f(2)
f(6)=f(2)*f(3)
f(3)=1
f(2)=1

状态转换方程为：

\(f(a*b)= \begin{array}{ll}
f(a)*f(b)*2+1 & a!=b，a为左子树b为右子树，和a为右子树b为左子树\\
f(a)*f(b)+1, & a==b\\
\end{array}\)

那最后的问题就是查找在index属于[0,i-1]的数组中，哪些a,b满足arr[a]*arr[b]==arr[i]，我们就可以使用上面提到的巧妙的方法类比解决该问题。这里就不再赘述。

解题代码和注释

func numFactoredBinaryTrees(arr []int) int {
    sort.Ints(arr)
    dp := make([]int64, len(arr))
    res, mod := int64(0), int64(1e9 + 7)
    for i := 0; i < len(arr); i++ {
        dp[i] = 1
        // 查找arr[left]*arr[right]==arr[right]*arr[left]
        for left, right := 0, i - 1; left <= right; left++ {
            for left <= right && int64(arr[left]) * int64(arr[right]) > int64(arr[i]) {
                right--
            }
            if left <= right && int64(arr[left]) * int64(arr[right]) == int64(arr[i]) {
                if left == right {
                    dp[i] = (dp[i] + dp[left] * dp[right]) % mod
                } else {
                    dp[i] = (dp[i] + dp[left] * dp[right] * 2) % mod
                }
            }
        }
        res = (res + dp[i]) % mod
    }
    return int(res)
}