Simulink仿真入门到精通（十二） Publish发布M文件

12.1 M文件的注释

使用%进行注释。

连续多行注释Ctrl+R，取消注释Ctrl+T。

12.2 Cell模式

在MATLAB脚本文件中使用连续两个注释符，开启一个新的Cell块，%%后空一格追加注释语句，所在行以粗体字显示。当前选中的Cell区域以淡橙色背景展示。

单击运行节（Ctrl+Alt+Enter）可以单独运行某一个Cell，方便调试。

12.3 注释的Publish

doc step

其实MATLAB的help文档就是从代码中产生的，只不过不是一般的代码，而是純注释。

注释生成文档源自MATLAB的Publish功能，可将注释文件生成.doc、.html等常用格式文件。当我们将注释按照一定的规则书写的时候，就可以自动生成所期望的漂亮规范的文本。

12.3.1 正文

>> publish('example')

ans =

    'C:\Users\lenovo\Desktop\html\example.html'

12.3.2 字体控制

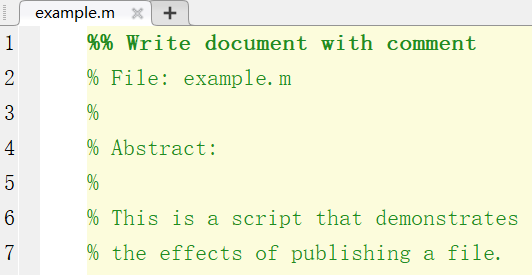
在正文两端增加'_'或'*'符号，可以得到斜体字和粗体字效果。

12.3.3 小标题

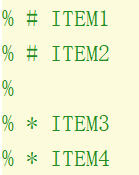
在%注释后加*符号和空格，生成点开头的标题；在%注释后加#符号和空格，生成数字序号列表。单独的%行会打断数字的连续性。

12.3.4 插入超链接

将网址用< >括住，在网址后空一格输入希望显示的文字。

12.3.5 插入可执行代码

% Please press <MATLAB:run('example.m') Run example code> to run
% the m script demo file.
a = 1;
b = 2;

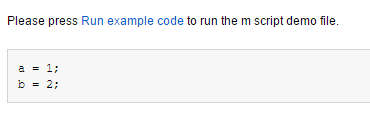
在MATLAB中打开后，单击链接即可执行脚本内容。

%% Publish codes with execution results.

for i=1:4
    imagesc(rand(6,6));
    snapnow;
end 

% run open(publish('chap12_03_11.m')) in Command window.

发布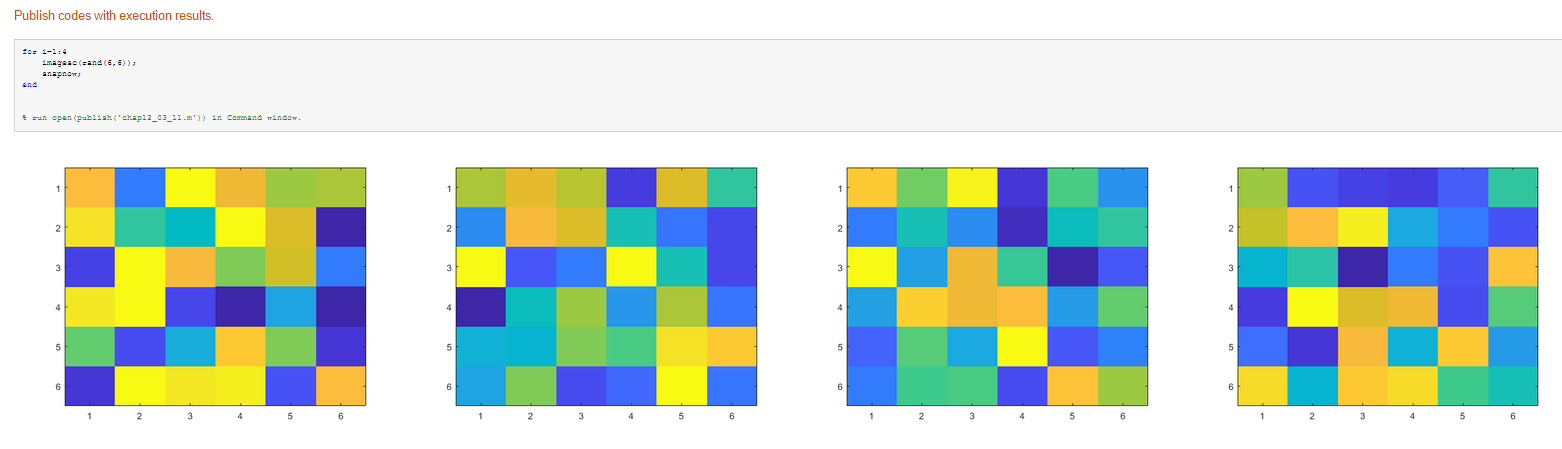

12.4 注释发布功能的应用场景

注释发布的功能不仅支持html类型，Doc、PPT等也都在Publish支持范围内。