Dijkstra学习总结

啥叫堆可以看一下这个 https://www.cnblogs.com/xiugeng/p/9645972.html#_label0
普通Dijkstra可以看一下 https://blog.csdn.net/weixin_42488861/article/details/97394821
堆优化的进阶 https://blog.csdn.net/scar_halo/article/details/82825418
大佬的堆优化 https://blog.csdn.net/major_zhang/article/details/72519233

那么堆优化又是咋优化，一般是使用STL的优先队列priority_queue实现的，本来普通Dijkstra算法所需时间复杂度为O(v^2),v为路径的数量。
使用了堆优化之后，所需要的时间复杂度为**O(E*logV),** E为顶点数量,为什么呢，因为堆操作所需要的时间复杂度为O(logV),堆优化还采用了邻接表形式存储相邻顶点，更新路径操作有O(E)次，把每个顶点当前的最短路径用堆维护。

顺便提一句，Dijkstra不能处理含有负权的图，为什么呢

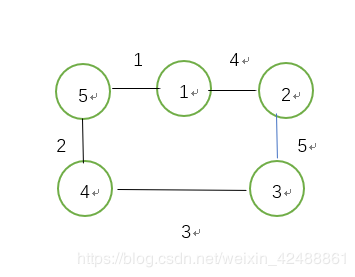
如图所示，若用Dijkstra处理，则第一次标记的是点2，距离为3，并且无法再更新，然而实际上点2的距离应该是通过3去松弛，距离为-1，1->3->2才是最优结果.
所以遇到具有负权的图应该用bellman-ford或者spfa处理

如何挑选应该使用的最短路算法：

①当权值为非负时，用Dijkstra。
②当权值有负值，且没有负圈，则用SPFA，SPFA能检测负圈，但是不能输出负圈。
③当权值有负值，而且可能存在负圈，则用BellmanFord，能够检测并输出负圈。
④SPFA和bellman-ford检测负环：当存在一个点入队大于等于V次时，则有负环。

Dijkstra与spfa的区别：

Dijkstra适用于稠密图，而spfa适用于稀疏图，但尽量不要使用spfa容易被卡数据，建议稀疏图使用dijkstra堆优化
spfa时间复杂度为O(kE) ->O(VE),k为期望值<=2，最差的情况下是O(VE)
**稀疏图和稠密图**的定义：
数据结构中对于稀疏图的定义为：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph），反之边的条数|E|接近|V|²，称为稠密图（dense graph）。

详情见于
https://www.cnblogs.com/flipped/p/6830073.html

来看一道题目:
https://vjudge.net/problem/POJ-3255

Descriptions

Bessie搬到了一个新的农场，有时候他会回去看他的老朋友。但是他不想很快的回去，他喜欢欣赏沿途的风景，所以他会选择次短路，因为她知道一定有一条次短路。
这个乡村有R(1<=R<=100000)条双向道路，每一条连接N(1<=N<=5000)个点中的两个。Bessie在1号节点，他的朋友家是n号节点Input第一行：两个整数N和R
接下来R行:每行包含三个整数，A，B,D，表示一条连接A与B的长度为D的路径Output输出1到n的次短路

Sample Input

4 4
1 2 100
2 4 200
2 3 250
3 4 100
Sample Output

450
Hint

两条路线：1 - > 2 - > 4（长度100 + 200 = 300）和1 - > 2 - > 3 - > 4（长度100 + 250 + 100 = 450）

AC代码：

 #include<iostream>
 #include<cstring>
 #include<math.h>
 #include<stdlib.h>
 #include<cstring>
 #include<cstdio>
 #include<utility>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 const int inf=0x3f3f3f3f;
 ;
 struct edge{
     int to,cost;
 };
 int n,m;
 typedef pair<int ,int>p;///first 是最短距离 second是顶点
 vector<edge>G[maxn];//邻接表
 ],e[][],vis[],dis2[];
 void dijkstra(){
     priority_queue<p,vector<p>,greater<p> >q;
     memset(dis,inf,sizeof(dis));
     memset(dis2,inf,sizeof(dis2));
     dis[]=;
     q.push(p(,));
     while(!q.empty()){
         p now=q.top();q.pop();
         int v=now.second,d=now.first;
         if(dis2[v]<d)continue;

         ;i<G[v].size();i++){//v连接了几个点
             edge e=G[v][i];
             int d2=d+e.cost;//当前点的最短距离加上与相邻点的距离
             if(dis[e.to]>d2){
                 swap(dis[e.to],d2);//松弛
                 q.push(p(dis[e.to],e.to));
             }
             if(dis2[e.to]>d2&&dis[e.to]<d2){
                 dis2[e.to]=d2;
                 q.push(p(dis2[e.to],e.to));
             }
         } 

     }
     cout<<dis2[n];

 }
 int main( )
 {
     ios::sync_with_stdio(false);
     cin.tie();
     int from;
     while(cin>>n>>m){

         edge now;
         ;i<=m;i++){
             cin>>from>>now.to>>now.cost;

             G[from].push_back(now);

             swap(now.to,from);

             G[from].push_back(now);

         }
         dijkstra(); 

     }

     ;
 }