编译原理_P1003

1.　　语法分析

1.1　　上下文无关文法的定义

----  正规式能定义一下简单的语言，能表示给定结构的固定次数的重复或者没有指定次数的重复

　　例如：a(ba)5,a(ba)*

---- 正规式不能用于描述配对或嵌套的结构

　　例如1：配对括号串的集合

　　例如2：{wcw|w是a和b的串}

1.2　　上下文无关文法是四元组（V_T，V_N，S,P）

　　终结符集合

　　非终结符集合

　　开始符号，非终结符中的一个

　　产生式集合，产生式形式：A→α

分析树

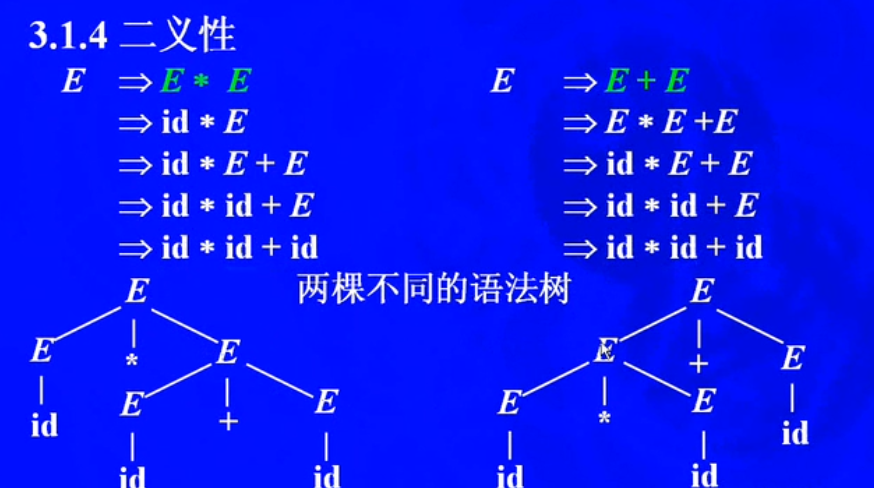
二义性

对结构有两种不同的观点

2.　　语言和文法

* 文法的优点

---- 文法给出了精确的，易于理解的语法说明

----- 自动产生高效的分析器

----- 可以给出语言定义出层次结构

----- 以文法为基础的语言的实现便于语言的修改

* 文法的问题

---- 文法只能描述编程语言的大部分语法，不能描述语言中上下文有关的语法特征

2.1　　正规式和上下文无关文法的比较

2.2　　分离词法分析器理由

* 为什么要用正规式定义词法

---- 词法规则非常简单，不必用上下文无关文法

---- 对于词法记号，正规式描述简介且易于理解

从软件工程角度看，词法分析和语法分析的分离有如下好处

---- 简化设计

----- 编译器的效率会改进

---- 编译器的可移植性加强

---- 便于编译器前段的模块划分

* 是否把词法分析并与语法分析中，直接从字符流进行语法分析

---- 若把词法分析和语法分析合在一起，则必须将语言的注释和空白的规则反应在文法中，文法将大大复杂

---- 注解和空白由自己来处理的分析器，比注解和空格已由词法分析器删除的分析器要复杂得多

2.3　　验证文法产生的语言

2.4　　适当的表达式文法

2.5　　消除二义性

2.6　　消除左递归