Dynamic Programming: From novice to advanced

出处：http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=dynProg

An important part of given problems can be solved with the help of dynamic programming (DP for short). Being able to tackle problems of this type would greatly increase your skill.I will try to help you in understanding how to solve problems
using DP. The article is based on examples, because a raw theory is very hard to understand.

Note: If you're bored reading one section and you already know what's being discussed in it - skip it and go to the next one.

Introduction (Beginner)

What is a dynamic programming, how can it be described?

A DP is an algorithmic technique which is usually based on a recurrent formula and one (or some) starting states. A sub-solution of the problem is constructed from previously found ones.DP solutions have a polynomial complexity which assures
a much faster running time than other techniques like backtracking, brute-force etc.

Now let's see the base of DP with the help of an example:

Given a list of N coins, their values (V₁, V₂, ... ,V_N), and the total sum
S. Find the minimum number of coins the sum of which isS (we can use as many coins of one type as we want), or report that it's not possible to select coins in such a way that they sum up toS.

Now let's start constructing a DP solution:

First of all we need to find a state for which an optimal solution is found and with the help of which we can find the optimal solution for the next state.

What does a "state" stand for?

It's a way to describe a situation, a sub-solution for the problem. For example a state would be the solution for sumi, where
i≤S. A smaller state than state i would be the solution for any sum
j, where j<i. For finding astate i, we need to first find all smaller states
j (j<i). Having found the minimum number of coins which sum up to
i, we can easily find the next state - the solution fori+1.

How can we find it?

It is simple - for each coin j, V_j≤i, look at the minimum number of coins found for thei-V_jsum (we have already found it previously). Let this number bem. If
m+1 is less than the minimum number of coins already found for current sumi, then we write the new result for it.

For a better understanding let's take this example:
Given coins with values 1, 3, and 5.
And the sum S is set to be 11.

First of all we mark that for state 0 (sum 0) we have found a solution with a minimum number of 0 coins.We then go to sum 1. First, we mark that we haven't yet found a solution for this one (a value of Infinity would be fine). Then we see that only coin 1 is
less than or equal to the current sum. Analyzing it, we see that for sum 1-V₁= 0 we have a solution with 0 coins. Because we add one coin to this solution, we'll have a solution with 1 coin for sum 1. It's the only solution yet
found for this sum. We write (save) it.Then we proceed to the next state -
sum 2. We again see that the only coin which is less or equal to this sum is the first coin, having a value of 1. The optimal solution found for sum (2-1) = 1 is coin 1. This coin 1 plus the first coin will sum up to 2, and thus make a sum of 2 with
the help of only 2 coins. This is the best and only solution for sum 2.Now we proceed to sum 3. We now have 2 coins which are to be analyzed - first and second one, having values of 1 and 3. Let's see the first one. There exists a solution for sum 2 (3 - 1)
and therefore we can construct from it a solution for sum 3 by adding the first coin to it. Because the best solution for sum 2 that we found has 2 coins, the new solution for sum 3 will have 3 coins.Now let's take the second coin with value equal to 3. The
sum for which this coin needs to be added to make 3 , is 0. We know that sum 0 is made up of 0 coins. Thus we can make a sum of 3 with only one coin - 3. We see that it's better than the previous found solution for sum 3 , which was composed of 3 coins. We
update it and mark it as having only 1 coin.The same we do for sum 4, and get a solution of 2 coins - 1+3. And so on.

Pseudocode:

Set Min[i] equal to Infinity for all of i

Min[0]=0

For i = 1 to S

For j = 0 to N - 1

   If (V

<=i AND Min[i-V

]+1<Min[i])

Then Min[i]=Min[i-V

]+1

Output Min[S]

Here are the solutions found for all sums:

Sum	Min. nr. of coins	Coin value added to a smaller sum to obtain this sum (it is displayed in brackets)
0	0	-
1	1	1 (0)
2	2	1 (1)
3	1	3 (0)
4	2	1 (3)
5	1	5 (0)
6	2	3 (3)
7	3	1 (6)
8	2	3 (5)
9	3	1 (8)
10	2	5 (5)
11	3	1 (10)

As a result we have found a solution of 3 coins which sum up to 11.

Additionally, by tracking data about how we got to a certain sum from a previous one, we can find what coins were used in building it. For example: to sum 11 we got by adding the coin with value 1 to a sum of 10. To sum 10 we got from 5. To 5 - from 0.This
way we find the coins used: 1, 5 and 5.

Having understood the basic way a DP is used, we may now see a slightly different approach to it. It involves the change (update) of best solution yet found for a sum i, whenever a better solution for this sum was found. In this case the states
aren't calculated consecutively.Let's consider the problem above. Start with having a solution of 0 coins for sum 0. Now let's try to add first coin (with value 1) to all sums already found. If the resulting sumt will be composed of fewer
coins than the one previously found - we'll update the solution for it. Then we do the same thing for the second coin, third coin, and so on for the rest of them.For example, we first add coin 1 to sum 0 and get sum 1. Because we haven't yet found a possible
way to make a sum of 1 - this is the best solution yet found, and we markS[1]=1. By adding the same coin to sum 1, we'll get sum 2, thus makingS[2]=2. And so on for the first coin.After the first coin is processed, take coin
2 (having a value of 3) and consecutively try to add it to each of the sums already found. Adding it to 0, a sum 3 made up of 1 coin will result. Till now,S[3] has been equal to 3, thus the new solution is better than the previously found
one. We update it and markS[3]=1. After adding the same coin to sum 1, we'll get a sum 4 composed of 2 coins. Previously we found a sum of 4 composed of 4 coins; having now found a better solution we updateS[4] to 2.The same
thing is done for next sums - each time a better solution is found, the results are updated.

Elementary

To this point, very simple examples have been discussed. Now let's see how to find a way for passing from one state to another, for harder problems. For that we will introduce a new term called recurrent relation, which makes a connection between a lower and
a greater state.

Let's see how it works:

Given a sequence of N numbers - A[1] , A[2] , ...,A[N]
. Find the length of the longest non-decreasing sequence.

As described above we must first find how to define a "state" which represents a sub-problem and thus we have to find a solution for it. Note that in most cases the states rely on lower states and are independent from greater states.

Let's define a state i as being the longest non-decreasing sequence which has its last numberA[i]
. This state carries only data about the length of this sequence. Note that fori<j the state
i is independent from j, i.e. doesn't change when we calculate statej. Let's see now how these states are connected to each other. Having found the solutions for all states lower thani, we
may now look for state i. At first we initialize it with a solution of 1, which consists only of thei-th number itself. Now for each
j<i let's see if it's possible to pass from it to state i. This is possible only whenA[j]≤A[i]
, thus keeping (assuring) the sequence non-decreasing. So ifS[j]
(the solution found for state j) + 1 (number
A[i] added to this sequence which ends with numberA[j]
) is better than a solution found for i (ie.S[j]+1>S[i]
), we make S[i]=S[j]+1.This way we consecutively find the best solutions for eachi, until last state N.

Let's see what happens for a randomly generated sequence: 5, 3, 4, 8, 6, 7:

I	The length of the longest non-decreasing sequence of first i numbers	The last sequence i from which we "arrived" to this one
1	1	1 (first number itself)
2	1	2 (second number itself)
3	2	2
4	3	3
5	3	3
6	4	5

Practice problem:
Given an undirected graph G having N (1<N<=1000) vertices and positive weights. Find the shortest path from vertex 1 to vertex N, or state that such path doesn't exist.

Hint: At each step, among the vertices which weren't yet checked and for which a path from vertex 1 was found, take the one which has the shortest path, from vertex 1 to it, yet found.

Try to solve the following problems from TopCoder competitions:

ZigZag - 2003 TCCC Semifinals 3
BadNeighbors - 2004 TCCC Round 4
FlowerGarden - 2004 TCCC Round 1

Intermediate

Let's see now how to tackle bi-dimensional DP problems.

Problem:
A table composed of N x M cells, each having a certain quantity of apples, is given.You start from the upper-left corner. At each step you can go down or right one cell.Find the maximum number of apples you can collect.

This problem is solved in the same way as other DP problems; there is almost no difference.

First of all we have to find a state. The first thing that must be observed is that there are at most 2 ways we can come to a cell - from the left (if it's not situated on the first column) and from the top (if it's not situated on the most upper row). Thus
to find the best solution for that cell, we have to have already found the best solutions for all of the cells from which we can arrive to the current cell.

From above, a recurrent relation can be easily obtained:
S[i][j]=A[i][j] + max(S[i-1][j], if i>0 ; S[i][j-1], if j>0) (wherei represents the row and
j the column of the table , its left-upper corner having coordinates {0,0} ; andA[i][j] being the number of apples situated in cell
i,j).

S[i][j] must be calculated by going first from left to right in each row and process the rows from top to bottom, or by going first from top to bottom in each column and process the columns from left to right.

Pseudocode:

For i = 0 to N - 1

   For j = 0 to M - 1

   S[i][j] = A[i][j] +

      max(S[i][j-1], if j>0 ; S[i-1][j], if i>0 ; 0)

Output S[n-1][m-1]

Here are a few problems, from TopCoder Competitions, for practicing:

AvoidRoads - 2003 TCO Semifinals 4
ChessMetric - 2003 TCCC Round 4

Upper-Intermediate

This section will discuss about dealing DP problems which have an additional condition besides the values that must be calculated.

As a good example would serve the following problem:

Given an undirected graph G having positive weights and
N vertices.

You start with having a sum of M money. For passing through a vertexi, you must pay
S[i] money. If you don't have enough money - you can't pass through that vertex.Find the shortest path from vertex 1 to vertex N, respecting the above conditions; or state that such path doesn't exist. If there exist more than one path having
the same length, then output the cheapest one.Restrictions: 1<N<=100 ; 0<=M<=100 ; for each i, 0<=S[i]<=100.As we can see, this is the same as the classical Dijkstra problem (finding the shortest path between two vertices), with the exception that it has a
condition.In the classical Dijkstra problem we would have used a uni-dimensional arrayMin[i]
, which marks the length of the shortest path found to vertexi.However in this problem we should also keep information about the money we have.Thus it would be reasonable to extend the array to something likeMin[i][j]
, which represents the length of the shortest path found to vertexi, with
j money being left. In this way the problem is reduced to the original path-finding algorithm.At each step we find the unmarked state (i,j) for which the shortest path was found. We mark it as visited (not to use it later), and for each of
its neighbors we look if the shortest path to it may be improved. If so - then update it.We repeat this step until there will remain no unmarked state to which a path was found. The solution will be represented byMin[N-1][j]
having the least value (and the greatest j possible among the states having the same value, i.e. the shortest paths to which has the same length).

Pseudocode:

Set states(i,j) as unvisited for all (i,j)

Set Min[i][j] to Infinity for all (i,j)

Min[0][M]=0

While(TRUE)

Among all unvisited states(i,j) find the one for which Min[i][j]

is the smallest. Let this state found be (k,l).

If there wasn't found any state (k,l) for which Min[k][l] is

less than Infinity - exit While loop.

Mark state(k,l) as visited

For All Neighbors p of Vertex k.

   If (l-S[p]>=0 AND

    Min[p][l-S[p]]>Min[k][l]+Dist[k][p])

      Then Min[p][l-S[p]]=Min[k][l]+Dist[k][p]

   i.e.

If for state(i,j) there are enough money left for

going to vertex p (l-S[p] represents the money that

will remain after passing to vertex p), and the

shortest path found for state(p,l-S[p]) is bigger

than [the shortest path found for

state(k,l)] + [distance from vertex k to vertex p)],

then set the shortest path for state(i,j) to be equal

to this sum.

End For

End While

Find the smallest number among Min[N-1][j] (for all j, 0<=j<=M);

if there are more than one such states, then take the one with greater

j. If there are no states(N-1,j) with value less than Infinity - then

such a path doesn't exist.

Here are a few TC problems for practicing:

Jewelry - 2003 TCO Online Round 4
StripePainter - SRM 150 Div 1
QuickSums - SRM 197 Div 2
ShortPalindromes - SRM 165 Div 2

Advanced

The following problems will need some good observations in order to reduce them to a dynamic solution.

Problem StarAdventure - SRM 208 Div 1:

Given a matrix with M rows and N columns (N x M). In each cell there's a number of apples.
You start from the upper-left corner of the matrix. You can go down or right one cell. You need to arrive to the bottom-right corner. Then you need to go back to the upper-left cell by going each step one cell left or up. Having arrived at this upper-left cell,
you need to go again back to the bottom-right cell.
Find the maximum number of apples you can collect.
When you pass through a cell - you collect all the apples left there.

Restrictions: 1 < N, M <= 50 ; each cell contains between 0 and 1000 apples inclusive.

First of all we observe that this problem resembles to the classical one (described in Section 3 of this article), in which you need to go only once from the top-left cell to the bottom-right one, collecting the maximum possible number of apples. It would be
better to try to reduce the problem to this one.Take a good look into the statement of the problem - what can be reduced or modified in a certain way to make it possible to solve using DP?First observation is that we can consider the second path (going from
bottom-right cell to the top-left cell) as a path which goes from top-left to bottom-right cell. It makes no difference, because a path passed from bottom to top, may be passed from top to bottom just in reverse order.In this way we get three paths going from
top to bottom. This somehow decreases the difficulty of the problem.We can consider these 3 paths as left, middle and right.When 2 paths intersect (like in the figure below)

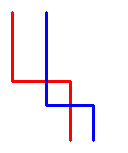
we may consider them as in the following picture, without affecting the result:

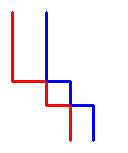
This way we'll get 3 paths, which we may consider as being one left, one middle and the other - right. More than that, we may see that for getting an optimal results they must not intersect (except in the leftmost upper corner and rightmost bottom corner).
So for each row y (except first and last), the x coordinates of the lines (x1[y],
x2[y] and respectively x3[y] ) will be :x1[y]
< x2[y] < x3[y] .Having done that - the DP solution now becomes much clearer. Let's consider the row y. Now suppose that for any configuration ofx1[y-1]
, x2[y-1] and x3[y-1] we have already found the paths which collect the maximum number of apples. From them we can find the optimal solution for rowy.We now have to find only the way for passing from
one row to the next one.LetMax[i][j][k] represent the maximum number of apples collected till rowy-1 inclusive, with three paths finishing at column
i,j, and respectively k. For the next row
y, add to each Max[i][j][k] (obtained previously) the number of apples situated in cells (y,i) , (y,j) and (y,k). Thus we move down at each step. After we made such a move,
we must consider that the paths may move in a row to the right.For keeping the paths out of an intersection, we must first consider the move to the right of the left path, after this of the middle path, and then of the right path. For a better understanding
think about the move to the right of the left path - take every possible pair of,
k (where j<k), and for each i (1 i<j) consider the move from position (i-1,j,k) to position (i,j,k). Having done this for the left path, start processing the middle one, which is done similarly;
and then process the right path.

TC problems for practicing:

MiniPaint - SRM 178 Div 1

Additional Note:
When have read the description of a problem and started to solve it, first look at its restrictions. If a polynomial-time algorithm should be developed, then it's possible that the solution may be of DP type. In this case try to see if there exist such states
(sub-solutions) with the help of which the next states (sub-solutions) may be found. Having found that - think about how to pass from one state to another. If it seems to be a DP problem, but you can't define such states, then try to reduce the problem to
another one (like in the example above, from Section 5).

Mentioned in this writeup:
TCCC '03 Semifinals 3 Div I Easy - ZigZag
TCCC '04 Round 4 Div I Easy - BadNeighbors
TCCC '04 Round 1 Div I Med - FlowerGarden
TCO '03 Semifinals 4 Div I Easy - AvoidRoads
TCCC '03 Round 4 Div I Easy - ChessMetric
TCO '03 Round 4 Div I Med - Jewelry
SRM 150 Div I Med - StripePainter
SRM 197 Div II Hard - QuickSums
SRM 165 Div II Hard - ShortPalindromes
SRM 208 Div I Hard - StarAdventure
SRM 178 Div I Hard - MiniPaint

作者：Dumitru

出处：http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=dynProg

中文翻译：http://hawstein.com/posts/dp-novice-to-advanced.html