POJ1423 - Big Number(Stirling公式)

题目大意

求N!有多少位

题解

用公式直接秒杀。。。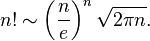

代码：

#include<iostream>
#include<cmath>
using namespace std;
#define ESP 1e-9
#define Pi acos(-1)
#define e exp(1.0)
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        int digit;
        double n;
        cin>>n;
        digit=(int)(ESP+0.5*log10(2*Pi*n)+n*log10(n/e))+1;
        cout<<digit<<endl;
    }
    return 0;
}