SGU 167.I-country

时间限制:0.75s

空间限制:65M

题意:

在一个n*m(n,m<=15)的网格中,每个格子有一个值,现在从网格中取出k(k<=n*m)个,保证在选中的格子中从任意一个格子去另外的所有格子最多只用到四种(上,下,左,右)操作中的两种，并使得到的值最大。输出该值和选中的格子坐标。

---

Solution

　　　　从选中的网格的任意一个去所有格子只用两种操作：

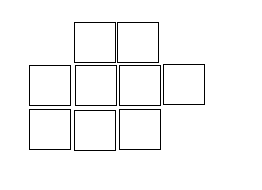
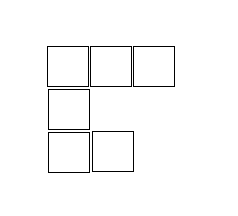
左图一种满足条件的网格集合，右图的（1，3）到（3,2）必需使用（左，下，右）三种操作才能到达，是不符合要求的。

注意到，满足条件的网格集合一定不会出现凹形，因为凹形的上下两个突出点中的格子不可能只用两个操作到达。

由此用0,1记录左右两边是 向外突出还是向内收缩。

当一行的一边向内收缩时便不可以再向外突出了。

接下来是按行dp

f[row][l][r][opl][opr][k],代表第row行,取第l列带第r列的格子,左边格子突出状态为opl,右边为opr,当前共选择了k个格子

记录路径时如果用结构体记录下所有的状态的上一个状态需要15*15*2*2*225 * size(int)*6的空间.

爆一次内存后,想到对于上一个状态row和k可以推出,只需要记录(l,r,opl,opr)即可,而(l,r,opl,opr)都是不超过16的数,那么可以用一个int形用16进制存下

存的时候用 record=(l << 12) + (r << 8) + (opl << 4) + (opr)

用的时候

上一个(row,l,r,opl,opr,k)

可以由当前的(row - 1, (record >> 12) % 16, (record >> 8) % 16, (record >> 4) % 16, record % 16, k - r + l - 1)得到

这道题需要注意的地方有很多,不一一列举.总的来说是一道值得一做的好题

参考代码:

#include <iostream>
#include <cstring>
#include <cstdio>
#define pdx pr[row][l][r][opl][opr][k]
#define val(r,a,b) g[r][b] - g[r][a - 1]
using namespace std;
int f[16][16][16][2][2][230], g[16][16];
int pr[16][16][16][2][2][230];
int n, m, k, ans;
int a, al, ar, aol, aor;
/*
       op=0    /  左突
       op=1    \  右突
*/
//当前状态向下更新
void update (int row, int l, int r, int opl, int opr, int s) {
	if (row == n) return ;
	for (int nl = (opl == 0 ? 1 : l); nl <= r; nl++)
		for (int nr = max (l, nl); nr <= (opr == 0 ? r : m); nr++) {
			int t1, t2;
			if (nl == l) t1 = opl;
			else
				t1 = (nl < l ? 0 : 1);
			if (nr == r) t2 = opr;
			else
				t2 = (nr < r ? 0 : 1);
			if (f[row + 1][nl][nr][t1][t2][s + (nr - nl + 1)] <
                              f[row][l][r][opl][opr][s] + val (row + 1, nl, nr) ) {
				f[row + 1][nl][nr][t1][t2][s + (nr - nl + 1)] =
                              f[row][l][r][opl][opr][s] + val (row + 1, nl, nr);
				//记录上一个状态   ,  16进制状态压缩
				pr[row + 1][nl][nr][t1][t2][s + (nr - nl + 1)] =
				              (l << 12) + (r << 8) + (opl << 4) + (opr);
			}
		}
}
 
void dp() {
	for (int row = 1; row <= n; row++)
		for (int l = 1; l <= m; l++)
			for (int r = l; r <= m; r++)
				for (int opl = 0; opl < 2; opl++)
					for (int opr = 0; opr < 2; opr++) {
						f[row][l][r][opl][opr][r - l + 1] = g[row][r] - g[row][l - 1];
						for (int s = r - l + 1; s <= k; s++)
							if (f[row][l][r][opl][opr][s] > 0 ) {
								update (row, l, r, opl, opr, s);
								if (s == k)//记录最大解
									if (f[row][l][r][opl][opr][s] > ans) {
										ans = f[row][l][r][opl][opr][s];
										a = row, al = l, ar = r, aol = opl, aor = opr;
									}
							}
					}
}
//输出
void write (int row, int l, int r, int opl, int opr, int k) {
	if (row == 0 || k <= 0) return;
	for (int i = l; i <= r; i++)
		printf ("%d %d\n", row, i);
	write (row - 1, (pdx >> 12) % 16, (pdx >> 8) % 16,
                      (pdx >> 4) % 16, pdx % 16, k - r + l - 1);
}
int main() {
#ifndef ONLINE_JUDGE
	freopen ("in.txt", "r", stdin);
#endif // oline_judge
	scanf ("%d %d %d", &n, &m, &k);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++) {
			scanf ("%d", &g[i][j]);
			g[i][j] += g[i][j - 1];
		}
	memset (f, -1, sizeof f);
	dp();
	printf ("Oil : %d\n", ans);
	write (a, al, ar, aol, aor, k);
	return 0;
}