leetcode-486-Predict the Winner

Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.

Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.

Example 1:

Input: [1, 5, 2]
Output: False
Explanation: Initially, player 1 can choose between 1 and 2. 
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2). 
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5. 
Hence, player 1 will never be the winner and you need to return False.

Example 2:

Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.

Note:

1. 1 <= length of the array <= 20.
2. Any scores in the given array are non-negative integers and will not exceed 10,000,000.
3. If the scores of both players are equal, then player 1 is still the winner.

思路：

参考自

http://www.voidcn.com/blog/starstar1992/article/p-6497962.html

https://discuss.leetcode.com/topic/76472/clean-3ms-c-dp-solution-with-detailed-explanation

https://discuss.leetcode.com/topic/76327/c-dp-solution-with-explanation

bool PredictTheWinner(vector<int>& nums)
     {
         int n = nums.size();
         vector<vector<int>>dp(n, vector<int>(n));
         vector<int>sum(n);
         sum[] = nums[];
         dp[][] = nums[];
         for (int i = ; i < n;i++)
         {
             sum[i] += sum[i - ] + nums[i];
             dp[i][i] = nums[i];
         }
         for (int i = ; i < n;i++)
         {
             for (int j = ; i + j < n;j++)
             {
                 dp[j][i + j] = max(sum[i+j]-sum[j]+nums[j] -dp[j+][i+j],sum[i+j]-sum[j]+nums[j]-dp[j][i+j-]);
             }
         }
         return  * dp[][n - ] >= sum[n - ];
     }

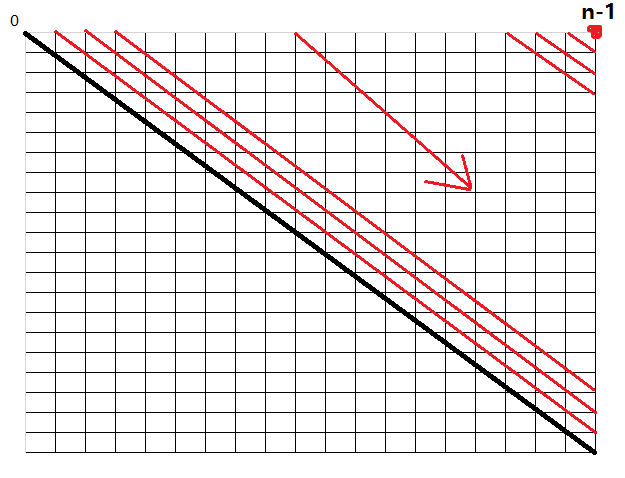
如上图所示，dp为二维数组，最终要求得是dp[0][n-1]那么，需要不断的去迭代更新dp[i][j]的值。求得过程类似上图，从对角线的上方

从左上到右下求dp[i][j]的值。也就是说求dp[i][j]需要用到它左边和下边的值 即左边dp[i][j-1]和下边dp[i+1][j]的值。

这一题用动态规划来解决。 
对于原数组A[0,….,n-1]，我们定义 
dp[i][j]表示原数组中从i到j的这么多数中，按照游戏规则，某个玩家所能获得的最大分数。 
假设这个分数此时属于palyer1，那么dp[i+1][j]或者dp[i][j-1]表示player2玩家所能获得的最大分数。因为对于player1来讲，他第一次选择要么是第i个数，要么是第j个数，所以对于player2来讲，就分两种情况取最大。

另外我们设从i到j的所有数的和是sum[i,j]，则可以得到递推公式：（动态规划最明显的标识） 
dp[i][j]=max(sum[i+1][j]-dp[i+1][j]+nums[i], sum[i][j-1]-dp[i][j-1]+nums[j]) 。

这个需要好好想想！其实不难！ 
化简一下： 
dp[i][j]=max(sum[i][j]-dp[i+1][j], sum[i][j]-dp[i][j-1]) 。

但是写代码实现时，我们要注意： 
首先要得到dp[i][i]的值，之后依次得到： 
dp[0][1],dp[1,2],dp[2,3]…dp[n-2][n-1] 
之后再得到dp[0][2],dp[1][3],…

for(int i=1;i<n;i++)
            for(int j=0;i+j<n;j++)
                dp[j][i+j]=max(sum[i+j]-sum[j]+nums[j]-dp[j+1][i+j],sum[i+j]-sum[j]+nums[j]-dp[j][i+j-1]);

所以这段代码的实现意图就比较明显了！ 
另外，注意sum[i+j]-sum[j]+nums[j]而不用sum[i+j]-sum[j-1]来求解从i到j的和，是为了考虑j=0时的情况。

细节处比较多，很考察能力！