【bzoj2618】[Cqoi2006]凸多边形 半平面交

题目描述

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：

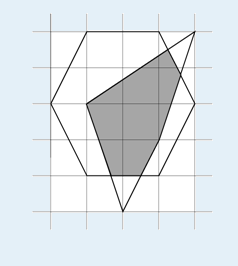
则相交部分的面积为5.233。

输入

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数m_i，表示多边形的边数，以下m_i行每行两个整数，逆时针给出各个顶点的坐标。

输出

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

样例输入

2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0

样例输出

5.233

---

题解

半平面交

题意即求一堆半平面的公共部分，即半平面交。

暴力半平面交可以过，但还是学了一下双端队列求半平面交的方法：

不妨设直线的右侧为半平面，那么把所有半平面按照直线的极角从小到大排序，极角相同的仅保留限制条件最严格的，即最右侧的。

排序去重以后扫一遍所有直线，判断分别队尾交点和队头交点是否在当前直线左端，在的话就踢出双端队列。然后再把当前半平面压入双端队列队尾。

最后，队尾的交点与队首可能不满足条件，因此还要弹掉队尾不合法的部分。

求面积的话直接上叉积就可以了。

废话不多说，直接上代码：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define eps 1e-9
#define N 510
using namespace std;
struct point
{
	double x , y;
	point() {}
	point(double a , double b) {x = a , y = b;}
	point operator+(const point &a)const {return point(x + a.x , y + a.y);}
	point operator-(const point &a)const {return point(x - a.x , y - a.y);}
	point operator*(const double &a)const {return point(a * x , a * y);}
}p[N];
struct line
{
	point p , v;
	double ang;
}a[N] , q[N] , c[N];
inline double cross(point a , point b) {return a.x * b.y - a.y * b.x;}
inline bool left(line a , point b) {return cross(a.v , b - a.p) > eps;}
inline point inter(line a , line b)
{
	point u = a.p - b.p;
	double tmp = cross(b.v , u) / cross(a.v , b.v);
	return a.p + a.v * tmp;
}
bool cmp(const line &a , const line &b)
{
	return fabs(a.ang - b.ang) < eps ? left(a , b.p) : a.ang < b.ang;
}
int main()
{
	int n , i , j , m , cnt = 0 , tot = 1 , l = 1 , r = 1;
	double ans = 0;
	scanf("%d" , &n);
	for(i = 1 ; i <= n ; i ++ )
	{
		scanf("%d" , &m);
		for(j = 1 ; j <= m ; j ++ ) scanf("%lf%lf" , &p[j].x , &p[j].y);
		for(j = 1 ; j <= m ; j ++ ) a[++cnt].p = p[j] , a[cnt].v = p[j] - p[j % m + 1] , a[cnt].ang = atan2(a[cnt].v.y , a[cnt].v.x);
	}
	sort(a + 1 , a + cnt + 1 , cmp);
	for(i = 2 ; i <= cnt ; i ++ )
		if(fabs(a[i].ang - a[i - 1].ang) > eps)
			a[++tot] = a[i];
	q[1] = a[1];
	for(i = 2 ; i <= tot ; i ++ )
	{
		while(l < r && left(a[i] , p[r - 1])) r -- ;
		while(l < r && left(a[i] , p[l])) l ++ ;
		q[++r] = a[i];
		if(l < r) p[r - 1] = inter(q[r - 1] , q[r]);
	}
	while(l < r && left(q[l] , p[r - 1])) r -- ;
	p[r] = inter(q[l] , q[r]) , p[r + 1] = p[l];
	for(i = l ; i <= r ; i ++ ) ans += cross(p[i] , p[i + 1]);
	printf("%.3lf\n" , ans / 2);
	return 0;
}