POJ 2391 Ombrophobic Bovines ( 经典最大流 && Floyd && 二分 && 拆点建图)

题意 : 给出一些牛棚，每个牛棚都原本都有一些牛但是每个牛棚可以容纳的牛都是有限的，现在给出一些路与路的花费和牛棚拥有的牛和可以容纳牛的数量，要求最短能在多少时间内使得每头牛都有安身的牛棚。( 这里注意给出的边是无向边且有重边 )

分析 : 听说是网络流的经典题型，这里先来讲一下如何转化为最大流然后二分求解。

① 先来说一下最大流在这题 ”扮演的角色"

先不考虑牛棚之间花费的关系，先抽象出原本没有的两个点，一个源点和一个汇点，设置源点到各个牛棚边的容量为牛棚原有的牛数，设置各个牛棚到汇点边的容量为各个牛棚的容量，然后将之间有路连接的牛棚都连上一条容量为无穷大的边 ( 但是后面实际不会这样做，需要拆点，现在可以先这样理解 )，这样建图后从源点到汇点跑出来的最大流如果等于全部牛的数量则说明可行 ( 即满流情况 )，否则不行。至此我们知道可以利用最大流的知识来判断当前建的一副图是否是一个可行解，由于时间越多满足条件的可能性越大，所以可以二分时间再用最大流来作为判断工具检查当前二分出来的时间是否可行。

② 和最短路算法的关系

既然现在是二分时间，那么必定有一些边是无法走的或者说有些点是不可互达的 ( 这些不符合条件的边或者两点间花费是大于当前二分出来的时间的 )，那么就要求求出这些两点间的最小花费，自然想到 Floyd 算法求全源最短路，每一次二分答案都根据 Floyd 跑出来的结果重新建图去跑最大流检查可行性 ( 但是具体要怎么做呢？不妨现在暂停一下想想？ )

③ 具体实现以及为何拆点建图？

其实根据刚刚 ①、② 的叙述，你可能？会想为什么不用最小费用最大流来求解呢？为什么要重新建图再跑最大流？

这里的时间是个时间覆盖问题，也就是说在给出的时间内可能有多头牛从不同点在进行移动！！这和在路径上跑出来的花费积累是不一样的！！仔细想想！！

在根据二分时间建图的过程中，如果就直接在原图上建，是起不到限制的作用的！以下引用 此论文 的解释

一种错误的建图方法，即不拆点，见下图：

其中每条无向边表示两条方向相反的有向边，容量均为∞。

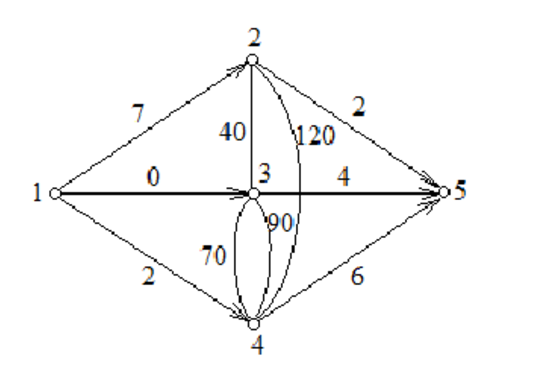
( 1 为源点、5 为汇点 )

当二分到 T = 70的时候，显然我们只加入了 (2, 3) 和 (3, 4) 两条无向边，因为只有这两对点间的最短距离小于等于 70。

但是从图中也可以看出，由于没有拆点，点 2 也可以通过这两条边到达点 4，而实际上这是不允许的。也就是说我们所加

的限制条件没有起到作用。由此可见，只有拆点才是正确的做法。

拆点的正确做法则是将原本的 v 点拆成 v 与 v' ，源点和各个 v 相连、汇点和各个 v'

如果 Dis[u][v] <= 当前二分时间 则连 u 与 v' ，就避免了与 v 相连产生干扰。

其实这样连出来的图为一个二分图 or 二部图。

代码实现则是多开 N 个点即可，即 原本编号为 1~n 的点拆成 1~n 和 n+1~2*n ，此时 v' = v + n

其实这题最后就归结为最大流下的最大距离最小化问题，一般此种类型都用二分解决。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
;
const int INF  = 1e9;
;
LL Dist[maxn][maxn];
int Have[maxn], Can[maxn];
int N, M;
int Full_Flow;
LL Limit;

struct Edge
{
    Edge(){}
    Edge(int from,int to,int cap,int flow):from(from),to(to),cap(cap),flow(flow){}
    int from,to,cap,flow;
};

struct Dinic
{
    int n,m,s,t;            //结点数,边数(包括反向弧),源点与汇点编号
    vector<Edge> edges;     //边表 edges[e]和edges[e^1]互为反向弧
    vector<int> G[maxn];    //邻接表,G[i][j]表示结点i的第j条边在e数组中的序号
    bool vis[maxn];         //BFS使用,标记一个节点是否被遍历过
    int d[maxn];            //d[i]表从起点s到i点的距离(层次)
    int cur[maxn];          //cur[i]表当前正访问i节点的第cur[i]条弧

    void init(int n,int s,int t)
    {
        this->n=n,this->s=s,this->t=t;
        ;i<=n;i++) G[i].clear();
        edges.clear();
    }

    void AddEdge(int from,int to,int cap)
    {
        edges.push_back( Edge() );
        edges.push_back( Edge(to,,) );
        m = edges.size();
        G[);
        G[to].push_back(m-);
    }

    bool BFS()
    {
        memset(vis,,sizeof(vis));
        queue<int> Q;//用来保存节点编号的
        Q.push(s);
        d[s]=;
        vis[s]=true;
        while(!Q.empty())
        {
            int x=Q.front(); Q.pop();
            ; i<G[x].size(); i++)
            {
                Edge& e=edges[G[x][i]];
                if(!vis[e.to] && e.cap>e.flow)
                {
                    vis[e.to]=true;
                    d[e.to] = d[x]+;
                    Q.push(e.to);
                }
            }
        }
        return vis[t];
    }

    //a表示从s到x目前为止所有弧的最小残量
    //flow表示从x到t的最小残量
    int DFS(int x,int a)
    {
        //printf("%d %d\n", x, a);
        )return a;
        ,f;//flow用来记录从x到t的最小残量
        for(int& i=cur[x]; i<G[x].size(); i++)
        {
            Edge& e=edges[G[x][i]];
            ==d[e.to] && (f=DFS( e.to,min(a,e.cap-e.flow) ) )> )
            {
                e.flow +=f;
                edges[G[x][i]^].flow -=f;
                flow += f;
                a -= f;
                ) break;
            }
        }
        return flow;
    }

    int Maxflow()
    {
        ;
        while(BFS())
        {
            memset(cur,,sizeof(cur));
            flow += DFS(s,INF);
        }
        return flow;
    }
}DC;

bool OK(LL Upper)
{
    DC.init(*N+, , *N+);
    ; i<=N; i++){
        DC.AddEdge(, i, Have[i]);
        DC.AddEdge(i+N, *N+, Can[i]);
    }

    ; i<=N; i++)
        ; j<=N; j++)
            if(Dist[i][j] <= Upper)
                DC.AddEdge(i, j+N, INF);

    return (Full_Flow == DC.Maxflow());
}

int main(void)
{
    while(~scanf("%d %d", &N, &M)){
        Full_Flow = ;
        Limit = ;

        ; i<=N; i++){
            scanf("%d %d", &Have[i], &Can[i]);
            Full_Flow += Have[i];///记录所有牛的数量
        }

        ; i<=N; i++)
            ; j<=N; j++)///跑 Floyd 前的初始化
                ;
                else Dist[i][j] = INF_LL;

        int From, To;
        LL Cost;
        ; i<=M; i++){
            scanf("%d %d %lld", &From, &To, &Cost);
            Dist[From][To] = Dist[To][From] = min(Dist[From][To], Cost);///有重边，只需记录最小的花费那条边
        }

        ; k<=N; k++)///Floyd 算法
            ; i<=N; i++)
                ; j<=N; j++)
                    if(Dist[i][k] < INF_LL && Dist[k][j] < INF_LL)
                        Dist[i][j] = min(Dist[i][j], Dist[i][k]+Dist[k][j]);

        Limit = ;///再次强调这里的时间是覆盖时间，所以我们找出花费最大的两点互大花费作为二分上界
        ; i<=N; i++)
            ; j<=N; j++)
                if(Dist[i][j] < INF_LL)
                    Limit = max(Limit, Dist[i][j]);

        if(!OK(Limit)) puts("-1");///给出最充裕的时间都无法满流肯定是无解了
        else{
            LL L = , R = Limit, ans;
            while(L <= R){///二分答案
                LL mid = L + ((R-L)>>);
                ;
                ;
            }
            printf("%lld\n", ans);
        }
    }
    ;
}